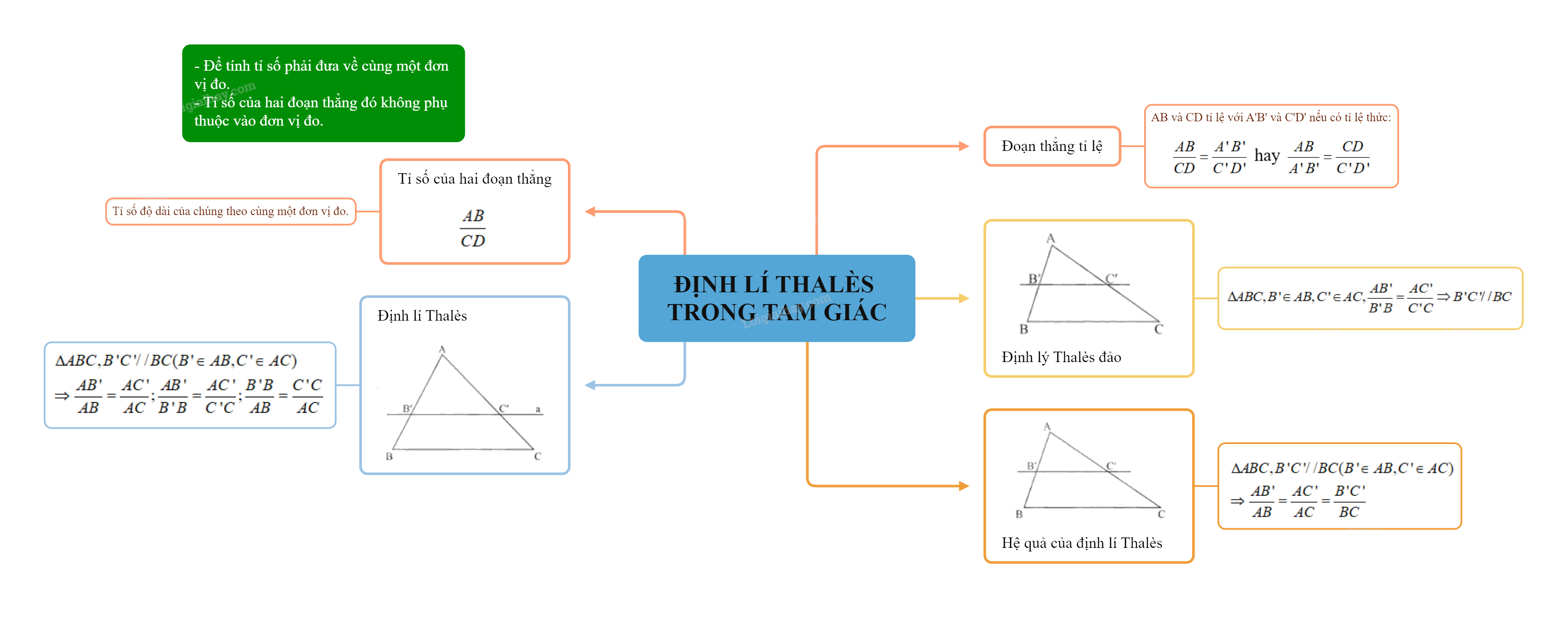
Định lí Thales là một trong những kiến thức quan trọng bậc nhất trong chương trình Toán 8, đặc biệt là sách Chân trời sáng tạo. Nắm vững định lí này không chỉ giúp bạn giải quyết các bài toán trong SGK mà còn là bước đệm vững chắc cho các kiến thức hình học nâng cao.
Tại giaitoan.edu.vn, chúng tôi cung cấp lý thuyết Định lí Thales được trình bày một cách dễ hiểu, kèm theo các ví dụ minh họa và bài tập thực hành đa dạng, giúp bạn tự tin chinh phục môn Toán.
Định lí Thales là gì?
1. Tỉ số của hai đoạn thẳng
Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là: \(\frac{{AB}}{{CD}}\)
Chú ý:
- Để tính tỉ số của hai đoạn thẳng, ta phải đưa chúng về cùng một đơn vị đo.
- Tỉ số của hai đoạn thẳng đó không phụ thuộc vào đơn vị đo độ dài đoạn thẳng.
Đoạn thẳng tỉ lệ
Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức: \(\frac{{AB}}{{CD}} = \frac{{A'B}}{{C'D}}\) hay \(\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\)
2. Định lí Thalès
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương đương tỉ lệ.
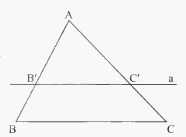
\(\begin{array}{l}\Delta ABC,B'C'//BC(B' \in AB,C' \in AC)\\ \Rightarrow \frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}};\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}};\frac{{B'B}}{{AB}} = \frac{{C'C}}{{AC}}\end{array}\) 3. Hệ quả của định lí Thalès
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
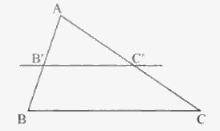
\(\begin{array}{l}\Delta ABC,B'C'//BC(B' \in AB,C' \in AC)\\ \Rightarrow \frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\end{array}\)
4. Định lí Thalès đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
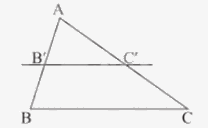
\(\Delta ABC,B' \in AB,C' \in AC,\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}} \Rightarrow B'C'//BC\)
Định lí Thales là một trong những định lý cơ bản và quan trọng trong hình học, được học trong chương trình Toán 8. Định lý này liên quan đến việc chia tỉ lệ các đoạn thẳng khi có các đường thẳng song song cắt các cạnh của một tam giác. Bài viết này sẽ trình bày chi tiết về lý thuyết Định lí Thales trong tam giác theo chương trình SGK Toán 8 Chân trời sáng tạo.
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó chia hai cạnh đó thành những đoạn thẳng tỉ lệ.
Cụ thể, cho tam giác ABC, đường thẳng d song song với BC cắt AB tại M và AC tại N. Khi đó:
Từ Định lí Thales, ta có thể suy ra một số hệ quả quan trọng:
Chứng minh Định lí Thales dựa trên việc sử dụng các tam giác đồng dạng. Cụ thể:
Định lí Thales có rất nhiều ứng dụng trong việc giải các bài toán hình học, đặc biệt là các bài toán liên quan đến tam giác đồng dạng và tỉ lệ thức. Một số ứng dụng phổ biến:
Bài 1: Cho tam giác ABC, M là một điểm trên AB, N là một điểm trên AC sao cho MN song song với BC. Biết AM = 4cm, MB = 6cm, AN = 5cm. Tính độ dài NC.
Giải:
Áp dụng Định lí Thales, ta có: AM/MB = AN/NC
=> 4/6 = 5/NC
=> NC = (5 * 6)/4 = 7.5cm
Bài 2: Cho tam giác ABC, MN song song với BC. Biết AM/AB = 2/5. Tính tỉ số MN/BC.
Giải:
Áp dụng hệ quả của Định lí Thales, ta có: MN/BC = AM/AB
=> MN/BC = 2/5
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Định lí Thales trong tam giác SGK Toán 8 Chân trời sáng tạo. Chúc bạn học tập tốt!