Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập mục 1 trang 12 SGK Toán 8 tập 1 – Chân trời sáng tạo. Bài viết này sẽ giúp các em học sinh hiểu rõ hơn về kiến thức và phương pháp giải bài tập, từ đó nâng cao kết quả học tập môn Toán.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và phù hợp với trình độ của học sinh. Hãy cùng theo dõi bài viết này để nắm vững kiến thức Toán 8 nhé!
Tại một công trình xây dựng, người ta dùng ba loại tấm kính chống nắng , và với các kích thước như Hình 1 (tính bằng m). Giá tiền các tấm kính được tính theo diện tích với đơn giá đồng/ . Tại đây có hai lần nhập vật liệu như bảng sau:
Video hướng dẫn giải
Cho hai đa thức \(M = 1 + 3xy - 2{x^2}{y^2}\) và \(N = x - xy + 2{x^2}{y^2}\). Tính \(M + N\) và \(M - N\).
Phương pháp giải:
Muốn cộng hay trừ hai đa thức ta làm như sau:
- Viết hai đa thức trong ngoặc và nối với nhau bằng dấu cộng hay trừ.
- Bỏ dấu ngoặc rồi thu gọn đa thức thu được.
Lời giải chi tiết:
Ta có:
\(M + N = \left( {1 + 3xy - 2{x^2}{y^2}} \right) + \left( {x - xy + 2{x^2}{y^2}} \right)\)
\(M + N = 1 + 3xy - 2{x^2}{y^2} + x - xy + 2{x^2}{y^2}\)
\(M + N = \left( { - 2{x^2}{y^2} + 2{x^2}{y^2}} \right) + \left( {3xy - xy} \right) + x + 1\)
\(M + N = 2xy + x + 1\)
Ta có:
\(M - N = \left( {1 + 3xy - 2{x^2}{y^2}} \right) - \left( {x - xy + 2{x^2}{y^2}} \right)\)
\(M - N = 1 + 3xy - 2{x^2}{y^2} - x + xy - 2{x^2}{y^2}\)
\(M - N = \left( { - 2{x^2}{y^2} - 2{x^2}{y^2}} \right) + \left( {3xy + xy} \right) - x + 1\)
\(M - N = - 4{x^2}{y^2} + 4xy - x + 1\)
Video hướng dẫn giải
Tại một công trình xây dựng, người ta dùng ba loại tấm kính chống nắng \(A\), \(B\) và \(C\) với các kích thước như Hình 1 (tính bằng m). Giá tiền các tấm kính được tính theo diện tích với đơn giá \(a\) đồng/\({m^2}\). Tại đây có hai lần nhập vật liệu như bảng sau:
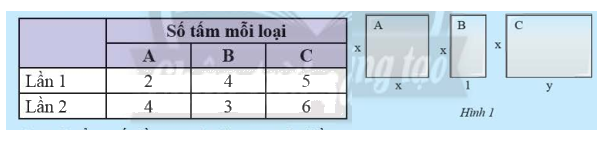
a) Tính tổng số tiền mua kính của cả hai lần.
b) Số tiền lần 2 nhiều hơn lần 1 bao nhiêu?
Phương pháp giải:
Sử dụng công thức tính diện tích hình vuông, hình chữ nhật để tính được số tiền mua kính.
Lời giải chi tiết:
a) Diện tích tấm kính chống nắng \(A\) là: \(x.x = {x^2}\) (\({m^2}\))
Diện tích tấm kính chống nắng \(B\) là: \(x.1 = x\) (\({m^2}\))
Diện tích tấm kính chống nắng \(C\) là: \(x.y = xy\) (\({m^2}\))
Số tiền mua kính lần 1 là: \(\left( {2{x^2} + 4x + 5xy} \right).a\) (đồng)
Số tiền mua kính lần 2 là: \(\left( {4{x^2} + 3x + 6xy} \right).a\) (đồng)
Tổng số tiền mua kính cả hai lần là: \(\left( {2{x^2} + 4x + 5xy} \right).a + \left( {4{x^2} + 3x + 6xy} \right).a = \left( {2{x^2} + 4x + 5xy + 4{x^2} + 3x + 6xy} \right).a = \left( {6{x^2} + 7x + 11xy} \right).a\)
b) Số tiền lần 2 nhiều hơn lần 1 là:
\(\left( {4{x^2} + 3x + 6xy} \right).a - \left( {2{x^2} + 4x + 5xy} \right).a = \left( {4{x^2} + 3x + 6xy - 2{x^2} - 4x - 5xy} \right).a = \left( {2{x^2} - x + xy} \right).a\)
Video hướng dẫn giải
Tại một công trình xây dựng, người ta dùng ba loại tấm kính chống nắng \(A\), \(B\) và \(C\) với các kích thước như Hình 1 (tính bằng m). Giá tiền các tấm kính được tính theo diện tích với đơn giá \(a\) đồng/\({m^2}\). Tại đây có hai lần nhập vật liệu như bảng sau:
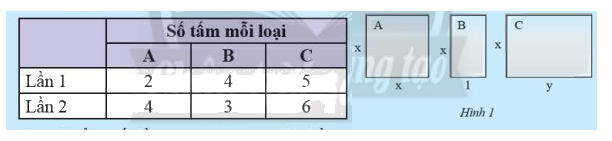
a) Tính tổng số tiền mua kính của cả hai lần.
b) Số tiền lần 2 nhiều hơn lần 1 bao nhiêu?
Phương pháp giải:
Sử dụng công thức tính diện tích hình vuông, hình chữ nhật để tính được số tiền mua kính.
Lời giải chi tiết:
a) Diện tích tấm kính chống nắng \(A\) là: \(x.x = {x^2}\) (\({m^2}\))
Diện tích tấm kính chống nắng \(B\) là: \(x.1 = x\) (\({m^2}\))
Diện tích tấm kính chống nắng \(C\) là: \(x.y = xy\) (\({m^2}\))
Số tiền mua kính lần 1 là: \(\left( {2{x^2} + 4x + 5xy} \right).a\) (đồng)
Số tiền mua kính lần 2 là: \(\left( {4{x^2} + 3x + 6xy} \right).a\) (đồng)
Tổng số tiền mua kính cả hai lần là: \(\left( {2{x^2} + 4x + 5xy} \right).a + \left( {4{x^2} + 3x + 6xy} \right).a = \left( {2{x^2} + 4x + 5xy + 4{x^2} + 3x + 6xy} \right).a = \left( {6{x^2} + 7x + 11xy} \right).a\)
b) Số tiền lần 2 nhiều hơn lần 1 là:
\(\left( {4{x^2} + 3x + 6xy} \right).a - \left( {2{x^2} + 4x + 5xy} \right).a = \left( {4{x^2} + 3x + 6xy - 2{x^2} - 4x - 5xy} \right).a = \left( {2{x^2} - x + xy} \right).a\)
Video hướng dẫn giải
Cho hai đa thức \(M = 1 + 3xy - 2{x^2}{y^2}\) và \(N = x - xy + 2{x^2}{y^2}\). Tính \(M + N\) và \(M - N\).
Phương pháp giải:
Muốn cộng hay trừ hai đa thức ta làm như sau:
- Viết hai đa thức trong ngoặc và nối với nhau bằng dấu cộng hay trừ.
- Bỏ dấu ngoặc rồi thu gọn đa thức thu được.
Lời giải chi tiết:
Ta có:
\(M + N = \left( {1 + 3xy - 2{x^2}{y^2}} \right) + \left( {x - xy + 2{x^2}{y^2}} \right)\)
\(M + N = 1 + 3xy - 2{x^2}{y^2} + x - xy + 2{x^2}{y^2}\)
\(M + N = \left( { - 2{x^2}{y^2} + 2{x^2}{y^2}} \right) + \left( {3xy - xy} \right) + x + 1\)
\(M + N = 2xy + x + 1\)
Ta có:
\(M - N = \left( {1 + 3xy - 2{x^2}{y^2}} \right) - \left( {x - xy + 2{x^2}{y^2}} \right)\)
\(M - N = 1 + 3xy - 2{x^2}{y^2} - x + xy - 2{x^2}{y^2}\)
\(M - N = \left( { - 2{x^2}{y^2} - 2{x^2}{y^2}} \right) + \left( {3xy + xy} \right) - x + 1\)
\(M - N = - 4{x^2}{y^2} + 4xy - x + 1\)
Mục 1 của chương trình Toán 8 tập 1 – Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về các phép toán cơ bản, các biểu thức đại số và các bài toán liên quan đến số thực. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài tập mục 1 trang 12 SGK Toán 8 tập 1 – Chân trời sáng tạo bao gồm các dạng bài tập sau:
Để tính giá trị của một biểu thức, ta cần thực hiện các phép toán theo đúng thứ tự ưu tiên: trong ngoặc trước, nhân chia trước, cộng trừ sau.
Ví dụ: Tính giá trị của biểu thức 2 + 3 * 4.
Ta thực hiện phép nhân trước: 3 * 4 = 12.
Sau đó thực hiện phép cộng: 2 + 12 = 14.
Vậy giá trị của biểu thức là 14.
Để rút gọn một biểu thức, ta cần thực hiện các phép toán để đưa biểu thức về dạng đơn giản nhất.
Ví dụ: Rút gọn biểu thức 3x + 2x - x.
Ta thực hiện phép cộng các số hạng đồng dạng: 3x + 2x = 5x.
Sau đó thực hiện phép trừ: 5x - x = 4x.
Vậy biểu thức được rút gọn là 4x.
Để giải một phương trình, ta cần tìm giá trị của ẩn số sao cho phương trình trở thành đúng.
Ví dụ: Giải phương trình 2x + 1 = 5.
Ta trừ cả hai vế của phương trình cho 1: 2x = 4.
Sau đó chia cả hai vế của phương trình cho 2: x = 2.
Vậy nghiệm của phương trình là x = 2.
Ngoài SGK Toán 8 tập 1 – Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên đây, các em học sinh sẽ tự tin hơn khi giải bài tập mục 1 trang 12 SGK Toán 8 tập 1 – Chân trời sáng tạo. Chúc các em học tập tốt!