Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 2 trang 11 và 12 của sách giáo khoa Toán 8 – Chân trời sáng tạo.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, rõ ràng và dễ tiếp thu nhất.
Bạn Khoa tìm được tấm bản đồ cổ cho biết kho báu của thuyền trưởng Độc Nhãn trên đảo Hòn Dừa (Hình 5) được dấu tại điểm có tọa độ (left( {6;4} right)). Em hãy kẻ một đường thẳng vuông góc với (Ox) tại điểm 6 và một đường thẳng vuông góc với (Oy) tại điểm 4. Xác định giao điểm của hai đường thẳng vừa vẽ để giúp bạn Khoa tìm kho báu.
Người ta có thể dùng hai số để xác định vị trí của một điểm trên mặt đất hoặc địa cầu, chẳng hạn Lý Sơn là một huyện đảo nổi tiếng của Việt Nam, nằm ở vị trí \(109^0 07'3''\)Đ, \(15^0 22'51''\)B. Em hãy lấy một bản đồ địa lí Việt Nam và xác định vị trí của đảo Lý Sơn theo kinh độ và vĩ độ.
Phương pháp giải:
Để xác định một điểm \(P\) có tọa độ là \(\left( {a;b} \right)\), ta thực hiện các bước sau:
- Tìm trên trục hoành điểm \(a\) và vẽ đường thẳng vuông góc với trục này tại điểm \(a\).
- Tìm trên trục tung điểm \(b\) và vẽ đường thẳng vuông góc với trục này tại điểm \(b\).
- Giao điểm của hai đường thẳng vừa vẽ cho ta điểm \(P\)cần tìm.
Lời giải chi tiết:
Học sinh tự thực hiện trên một bản đồ do thầy cô cung cấp.
Video hướng dẫn giải
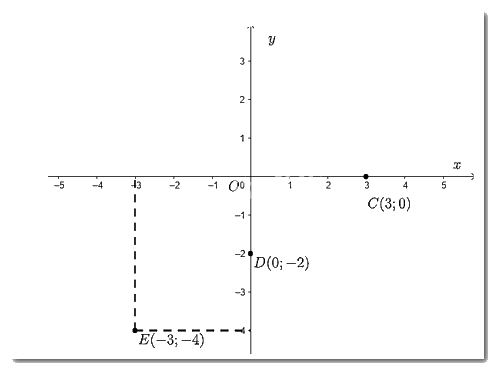
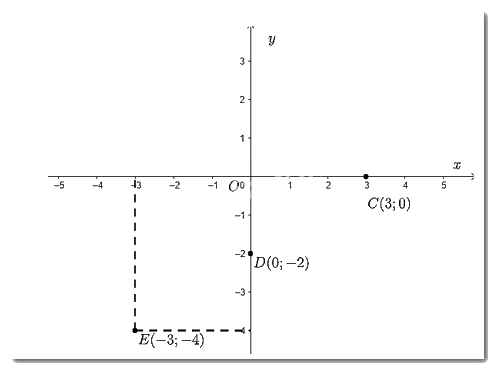
Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm \(C\left( {3;0} \right);D\left( {0; - 2} \right);E\left( { - 3; - 4} \right)\)
Phương pháp giải:
Để xác định một điểm \(P\) có tọa độ là \(\left( {a;b} \right)\), ta thực hiện các bước sau:
- Tìm trên trục hoành điểm \(a\) và vẽ đường thẳng vuông góc với trục này tại điểm \(a\).
- Tìm trên trục tung điểm \(b\) và vẽ đường thẳng vuông góc với trục này tại điểm \(b\).
- Giao điểm của hai đường thẳng vừa vẽ cho ta điểm \(P\)cần tìm.
Lời giải chi tiết:
- Đánh dấu điểm \(C\left( {3;0} \right)\)
Từ điểm 3 trên trục hoành ta vẽ đường thẳng vuông góc với \(Ox\); Từ điểm 0 trên trục tung ta vẽ đường thẳng vuông góc với \(Oy\) (chính là trục \(Ox\)). Giao điểm của hai đường thẳng này chính là điểm \(C\left( {3;0} \right)\);
- Đánh dấu điểm \(D\left( {0; - 2} \right)\)
Từ điểm 0 trên trục hoành ta vẽ đường thẳng vuông góc với \(Ox\)(chính là trục \(Oy\)); Từ điểm -2 trên trục tung ta vẽ đường thẳng vuông góc với \(Oy\). Giao điểm của hai đường thẳng này chính là điểm \(D\left( {0; - 2} \right)\).
- Đánh dấu điểm \(E\left( { - 3; - 4} \right)\)
Từ điểm -3 trên trục hoành ta vẽ đường thẳng vuông góc với \(Ox\); Từ điểm -4 trên trục tung ta vẽ đường thẳng vuông góc với \(Oy\). Giao điểm của hai đường thẳng này chính là điểm \(E\left( { - 3; - 4} \right)\).
Ta có hình vẽ
Video hướng dẫn giải
Bạn Khoa tìm được tấm bản đồ cổ cho biết kho báu của thuyền trưởng Độc Nhãn trên đảo Hòn Dừa (Hình 5) được dấu tại điểm có tọa độ \(\left( {6;4} \right)\). Em hãy kẻ một đường thẳng vuông góc với \(Ox\) tại điểm 6 và một đường thẳng vuông góc với \(Oy\) tại điểm 4. Xác định giao điểm của hai đường thẳng vừa vẽ để giúp bạn Khoa tìm kho báu.

Phương pháp giải:
Kẻ đường thẳng vuông góc với \(Ox\) tại điểm 6 và một đường thẳng vuông góc với \(Oy\) tại điểm 4. Hai đường thẳng cắt nhau tại giao điểm cần tìm.
Lời giải chi tiết:
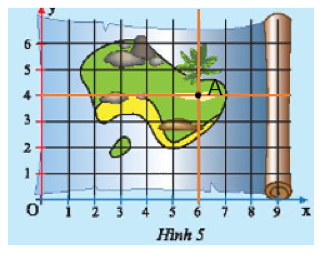
Đường thẳng vuông góc với \(Ox\) tại điểm 6 và đường thẳng vuông góc với \(Oy\) tại điểm 4 cắt nhau tại điểm \(A\) như hình vẽ.
Video hướng dẫn giải
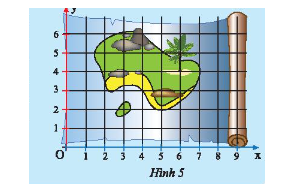
Bạn Khoa tìm được tấm bản đồ cổ cho biết kho báu của thuyền trưởng Độc Nhãn trên đảo Hòn Dừa (Hình 5) được dấu tại điểm có tọa độ \(\left( {6;4} \right)\). Em hãy kẻ một đường thẳng vuông góc với \(Ox\) tại điểm 6 và một đường thẳng vuông góc với \(Oy\) tại điểm 4. Xác định giao điểm của hai đường thẳng vừa vẽ để giúp bạn Khoa tìm kho báu.
Phương pháp giải:
Kẻ đường thẳng vuông góc với \(Ox\) tại điểm 6 và một đường thẳng vuông góc với \(Oy\) tại điểm 4. Hai đường thẳng cắt nhau tại giao điểm cần tìm.
Lời giải chi tiết:
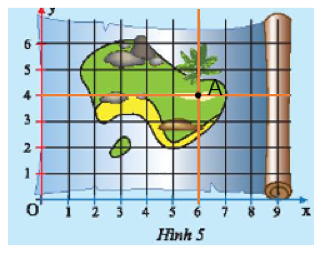
Đường thẳng vuông góc với \(Ox\) tại điểm 6 và đường thẳng vuông góc với \(Oy\) tại điểm 4 cắt nhau tại điểm \(A\) như hình vẽ.
Video hướng dẫn giải
Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm \(C\left( {3;0} \right);D\left( {0; - 2} \right);E\left( { - 3; - 4} \right)\)
Phương pháp giải:
Để xác định một điểm \(P\) có tọa độ là \(\left( {a;b} \right)\), ta thực hiện các bước sau:
- Tìm trên trục hoành điểm \(a\) và vẽ đường thẳng vuông góc với trục này tại điểm \(a\).
- Tìm trên trục tung điểm \(b\) và vẽ đường thẳng vuông góc với trục này tại điểm \(b\).
- Giao điểm của hai đường thẳng vừa vẽ cho ta điểm \(P\)cần tìm.
Lời giải chi tiết:
- Đánh dấu điểm \(C\left( {3;0} \right)\)
Từ điểm 3 trên trục hoành ta vẽ đường thẳng vuông góc với \(Ox\); Từ điểm 0 trên trục tung ta vẽ đường thẳng vuông góc với \(Oy\) (chính là trục \(Ox\)). Giao điểm của hai đường thẳng này chính là điểm \(C\left( {3;0} \right)\);
- Đánh dấu điểm \(D\left( {0; - 2} \right)\)
Từ điểm 0 trên trục hoành ta vẽ đường thẳng vuông góc với \(Ox\)(chính là trục \(Oy\)); Từ điểm -2 trên trục tung ta vẽ đường thẳng vuông góc với \(Oy\). Giao điểm của hai đường thẳng này chính là điểm \(D\left( {0; - 2} \right)\).
- Đánh dấu điểm \(E\left( { - 3; - 4} \right)\)
Từ điểm -3 trên trục hoành ta vẽ đường thẳng vuông góc với \(Ox\); Từ điểm -4 trên trục tung ta vẽ đường thẳng vuông góc với \(Oy\). Giao điểm của hai đường thẳng này chính là điểm \(E\left( { - 3; - 4} \right)\).
Ta có hình vẽ
Người ta có thể dùng hai số để xác định vị trí của một điểm trên mặt đất hoặc địa cầu, chẳng hạn Lý Sơn là một huyện đảo nổi tiếng của Việt Nam, nằm ở vị trí \(109^0 07'3''\)Đ, \(15^0 22'51''\)B. Em hãy lấy một bản đồ địa lí Việt Nam và xác định vị trí của đảo Lý Sơn theo kinh độ và vĩ độ.
Phương pháp giải:
Để xác định một điểm \(P\) có tọa độ là \(\left( {a;b} \right)\), ta thực hiện các bước sau:
- Tìm trên trục hoành điểm \(a\) và vẽ đường thẳng vuông góc với trục này tại điểm \(a\).
- Tìm trên trục tung điểm \(b\) và vẽ đường thẳng vuông góc với trục này tại điểm \(b\).
- Giao điểm của hai đường thẳng vừa vẽ cho ta điểm \(P\)cần tìm.
Lời giải chi tiết:
Học sinh tự thực hiện trên một bản đồ do thầy cô cung cấp.
Mục 2 của chương trình Toán 8 – Chân trời sáng tạo tập trung vào các kiến thức về đa thức. Cụ thể, học sinh sẽ được làm quen với các khái niệm như đơn thức, đa thức, bậc của đa thức, các phép toán trên đa thức (cộng, trừ, nhân, chia) và các ứng dụng của đa thức trong giải toán.
Bài tập này yêu cầu học sinh thu gọn các đa thức đã cho bằng cách thực hiện các phép toán cộng, trừ các đơn thức đồng dạng. Để thu gọn đa thức, ta cần:
Ví dụ: Thu gọn đa thức 3x2y + 5xy2 - 2x2y - xy2. Ta có:
3x2y - 2x2y + 5xy2 - xy2 = (3 - 2)x2y + (5 - 1)xy2 = x2y + 4xy2
Bậc của đa thức là bậc của đơn thức có bậc cao nhất trong đa thức đó. Để tìm bậc của đa thức, ta cần:
Ví dụ: Tìm bậc của đa thức 2x3y2 + 5x2y - 3xy + 1. Ta có:
Vậy, bậc của đa thức 2x3y2 + 5x2y - 3xy + 1 là 5.
Để cộng hoặc trừ hai đa thức, ta thực hiện các bước sau:
Ví dụ: Cộng hai đa thức A = 2x2y + 3xy2 - 5x2y2 và B = -x2y + 2xy2 - 3x2y2. Ta có:
A + B = (2x2y - x2y) + (3xy2 + 2xy2) + (-5x2y2 - 3x2y2) = x2y + 5xy2 - 8x2y2
Kiến thức về đa thức có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học và các ngành khoa học khác. Ví dụ:
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách giải mục 2 trang 11, 12 SGK Toán 8 – Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!