Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 7 trang 51 SGK Toán 8 tập 2 – Chân trời sáng tạo. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập về nhà.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải cụ thể, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho hình thang
Đề bài
Cho hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Chứng minh rằng \(OA.OD = OB.OC\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng hệ quả của định lí Thales.
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết
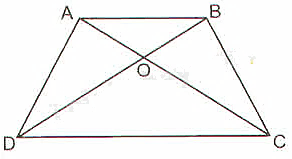
Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\) (điều phải chứng minh).
Bài 7 trang 51 SGK Toán 8 tập 2 – Chân trời sáng tạo thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về hình học và đại số để giải quyết các bài toán thực tế. Bài toán này thường yêu cầu học sinh phân tích đề bài, xác định các yếu tố cần tìm, và áp dụng các công thức, định lý phù hợp để tìm ra kết quả.
Thông thường, bài 7 trang 51 sẽ xoay quanh các chủ đề như:
Để giải bài 7 trang 51 SGK Toán 8 tập 2 – Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Bài toán: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Gọi E là trung điểm của AD. Đường thẳng EO cắt BC tại F. Chứng minh rằng BF = FC.
Giải:
Suy ra tam giác DOE đồng dạng với tam giác BOF (g-g).
Từ sự đồng dạng trên, ta có: DE/BF = DO/BO = 1 => DE = BF
Vì E là trung điểm của AD nên DE = AE. Do đó, BF = AE. Mà AE = DC (tính chất hình bình hành). Vậy BF = DC/2. Vì F là trung điểm của BC nên BF = FC. Do đó, BF = FC.
Trong quá trình giải bài tập, học sinh cần chú ý:
Để rèn luyện kỹ năng giải toán, học sinh có thể tham khảo các bài tập tương tự trong SGK Toán 8 tập 2 – Chân trời sáng tạo, hoặc tìm kiếm trên các trang web học toán trực tuyến.
Bài 7 trang 51 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình học và đại số. Bằng cách nắm vững phương pháp giải và rèn luyện thường xuyên, học sinh có thể tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn hy vọng bài viết này sẽ giúp ích cho các em học sinh trong quá trình học tập. Chúc các em học tốt!