Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 15, 16 SGK Toán 8 tập 1 – Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Mục tiêu của chúng tôi là hỗ trợ các em học tập hiệu quả, tiết kiệm thời gian và đạt kết quả tốt nhất trong môn Toán.
Hình chữ nhật (A) có chiều rộng (2x) (cm), chiều dài gấp (k) ((k > 1) lần chiều rộng. Hình chữ nhật (B) có chiều dài (3x) (cm). Muốn hai hình chữ nhật này có diện tích bằng nhau thì (B) phải có chiều rộng bằng bao nhiêu?
Video hướng dẫn giải
Tính diện tích đáy của hình hộp chữ nhật có thể tích \(V = 12{x^2}y\) và chiều cao bằng \(3y\).
Phương pháp giải:
Áp dụng quy tắc chia đơn thức cho đơn thức.
Áp dụng công thức tính diện tích đáy: \(S = V:h\) trong đó \(S\), \(V\), \(h\) lần lượt là diện tích đáy, thể tích, chiều cao của hình hộp chữ nhật.
Lời giải chi tiết:
Diện tích đáy của hình hộp chữ nhật là: \(12{x^2}y:\left( {3y} \right) = \left( {12:3} \right).\left( {y:y} \right).{x^2} = 4{x^2}\)
Video hướng dẫn giải
Thực hiện phép chia \(8{x^4}{y^5}{z^3}\) cho \(2{x^3}{y^4}z\).
Phương pháp giải:
Áp dụng quy tắc chia đơn thức cho đơn thức.
Lời giải chi tiết:
\(8{x^4}{y^5}{z^3}:\left( {2{x^3}{y^4}z} \right) = \left( {8:2} \right).\left( {{x^4}:{x^3}} \right).\left( {{y^5}:{y^4}} \right).\left( {{z^3}:z} \right) = 4xy{z^2}\)
Video hướng dẫn giải
Thực hiện các phép chia:
a) \(\left( {5ab - 2{a^2}} \right):a\)
b) \(\left( {6{x^2}{y^2} - x{y^2} + 3{x^2}y} \right): - 3xy\)
Phương pháp giải:
Áp dụng quy tắc chia đa thức cho đơn thức.
Lời giải chi tiết:
a) \(\left( {5ab - 2{a^2}} \right):a\)
\( = \left( {5ab:a} \right) - \left( {2{a^2}:a} \right)\)
\( = 5b - 2a\)
b) \(\left( {6{x^2}{y^2} - x{y^2} + 3{x^2}y} \right): - 3xy\)
\( = \left[ {6{x^2}{y^2}:\left( { - 3xy} \right)} \right] - \left[ {x{y^2}:\left( { - 3xy} \right)} \right] + \left[ {3{x^2}y:\left( { - 3xy} \right)} \right]\)
\( = - 2xy - \left( { - \frac{1}{3}y} \right) + \left( { - x} \right)\)
\( = - 2xy + \frac{1}{3}y - x\)
Video hướng dẫn giải
Tính chiều cao của hình hộp chữ nhật có thể tích \(V = 6{x^2}y - 8x{y^2}\) và diện tích đáy \(S = 2xy\).
Phương pháp giải:
Áp dụng công thức tính chiều cao hình hộp chữ nhật: \(h = V:S\) trong đó \(S\), \(V\), \(h\) lần lượt là diện tích đáy, thể tích, chiều cao của hình hộp chữ nhật.
Áp dụng quy tắc chia đa thức cho đơn thức.
Lời giải chi tiết:
Chiều cao của hình hộp chữ nhật là:
\(\left( {6{x^2}y - 8x{y^2}} \right):\left( {2xy} \right) = \left[ {6{x^2}y:\left( {2xy} \right)} \right] - \left[ {8x{y^2}:\left( {2xy} \right)} \right]\)\( = 3x - 4y\)
Video hướng dẫn giải
Một bức tường được trang trí bởi hai tấm giấy dán có cùng chiều cao \(2x\) (m) và có diện tích lần lượt là \(2{x^2}\) (\({m^2}\)) và \(5xy\) (\({m^2}\)).
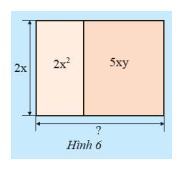
a) Tính chiều rộng của mỗi tấm giấy, từ đó tìm chiều rộng của bức tường.
b) Từ kết quả trên, có thể biết được kết quả của phép chia đa thức \(A = 2{x^2} + 5xy\) cho đơn thức \(B = 2x\) không? Hãy giải thích.
Phương pháp giải:
Áp dụng quy tắc chia đơn thức cho đơn thức.
Lời giải chi tiết:
a) Chiều rộng của tấm giấy thứ nhất là: \(2{x^2}:\left( {2x} \right) = \left( {2:2} \right).\left( {{x^2}:x} \right) = x\) (m)
Chiều rộng tấm giấy thứ hai là: \(5xy:\left( {2x} \right) = \left( {5:2} \right).\left( {x:x} \right).y = \frac{5}{2}y\) (m)
Chiều rộng của bức tường là: \(x + \frac{5}{2}y\) (m)
b) Kết quả của phép chia đa thức \(A = 2{x^2} + 5xy\) cho đa thức \(B = 2x\) là \(x + \frac{5}{2}y\)
Vì \(\left( {x + \frac{5}{2}y} \right).\left( {2x} \right) = x.2x + \frac{5}{2}y.2x = 2{x^2} + 5xy\)
Video hướng dẫn giải
Hình chữ nhật \(A\) có chiều rộng \(2x\) (cm), chiều dài gấp \(k\) (\(k > 1\) lần chiều rộng. Hình chữ nhật \(B\) có chiều dài \(3x\) (cm). Muốn hai hình chữ nhật này có diện tích bằng nhau thì \(B\) phải có chiều rộng bằng bao nhiêu?
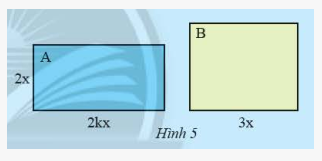
Phương pháp giải:
Áp dụng công thức tính diện tích hình chữ nhật.
Áp dụng quy tắc nhân đơn thức với đơn thức, chia đơn thức cho đơn thức.
Lời giải chi tiết:
Diện tích hình chữ nhật \(A\) là: \(2kx.2x = 4k{x^2}\) \(c{m^2}\)
Muốn hai hình chữ nhật \(A\) và \(B\) có diện tích bằng nhau thì chiều rộng hình chữ nhật \(B\) là:
\(4k{x^2}:\left( {3x} \right) = \left( {4:3} \right).\left( {{x^2}:x} \right).k = \frac{4}{3}xk\) (cm)
Video hướng dẫn giải
Hình chữ nhật \(A\) có chiều rộng \(2x\) (cm), chiều dài gấp \(k\) (\(k > 1\) lần chiều rộng. Hình chữ nhật \(B\) có chiều dài \(3x\) (cm). Muốn hai hình chữ nhật này có diện tích bằng nhau thì \(B\) phải có chiều rộng bằng bao nhiêu?
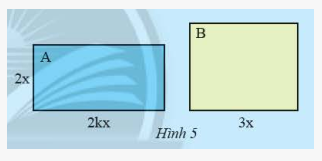
Phương pháp giải:
Áp dụng công thức tính diện tích hình chữ nhật.
Áp dụng quy tắc nhân đơn thức với đơn thức, chia đơn thức cho đơn thức.
Lời giải chi tiết:
Diện tích hình chữ nhật \(A\) là: \(2kx.2x = 4k{x^2}\) \(c{m^2}\)
Muốn hai hình chữ nhật \(A\) và \(B\) có diện tích bằng nhau thì chiều rộng hình chữ nhật \(B\) là:
\(4k{x^2}:\left( {3x} \right) = \left( {4:3} \right).\left( {{x^2}:x} \right).k = \frac{4}{3}xk\) (cm)
Video hướng dẫn giải
Thực hiện phép chia \(8{x^4}{y^5}{z^3}\) cho \(2{x^3}{y^4}z\).
Phương pháp giải:
Áp dụng quy tắc chia đơn thức cho đơn thức.
Lời giải chi tiết:
\(8{x^4}{y^5}{z^3}:\left( {2{x^3}{y^4}z} \right) = \left( {8:2} \right).\left( {{x^4}:{x^3}} \right).\left( {{y^5}:{y^4}} \right).\left( {{z^3}:z} \right) = 4xy{z^2}\)
Video hướng dẫn giải
Tính diện tích đáy của hình hộp chữ nhật có thể tích \(V = 12{x^2}y\) và chiều cao bằng \(3y\).
Phương pháp giải:
Áp dụng quy tắc chia đơn thức cho đơn thức.
Áp dụng công thức tính diện tích đáy: \(S = V:h\) trong đó \(S\), \(V\), \(h\) lần lượt là diện tích đáy, thể tích, chiều cao của hình hộp chữ nhật.
Lời giải chi tiết:
Diện tích đáy của hình hộp chữ nhật là: \(12{x^2}y:\left( {3y} \right) = \left( {12:3} \right).\left( {y:y} \right).{x^2} = 4{x^2}\)
Video hướng dẫn giải
Một bức tường được trang trí bởi hai tấm giấy dán có cùng chiều cao \(2x\) (m) và có diện tích lần lượt là \(2{x^2}\) (\({m^2}\)) và \(5xy\) (\({m^2}\)).
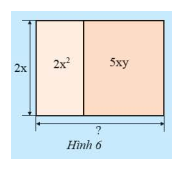
a) Tính chiều rộng của mỗi tấm giấy, từ đó tìm chiều rộng của bức tường.
b) Từ kết quả trên, có thể biết được kết quả của phép chia đa thức \(A = 2{x^2} + 5xy\) cho đơn thức \(B = 2x\) không? Hãy giải thích.
Phương pháp giải:
Áp dụng quy tắc chia đơn thức cho đơn thức.
Lời giải chi tiết:
a) Chiều rộng của tấm giấy thứ nhất là: \(2{x^2}:\left( {2x} \right) = \left( {2:2} \right).\left( {{x^2}:x} \right) = x\) (m)
Chiều rộng tấm giấy thứ hai là: \(5xy:\left( {2x} \right) = \left( {5:2} \right).\left( {x:x} \right).y = \frac{5}{2}y\) (m)
Chiều rộng của bức tường là: \(x + \frac{5}{2}y\) (m)
b) Kết quả của phép chia đa thức \(A = 2{x^2} + 5xy\) cho đa thức \(B = 2x\) là \(x + \frac{5}{2}y\)
Vì \(\left( {x + \frac{5}{2}y} \right).\left( {2x} \right) = x.2x + \frac{5}{2}y.2x = 2{x^2} + 5xy\)
Video hướng dẫn giải
Thực hiện các phép chia:
a) \(\left( {5ab - 2{a^2}} \right):a\)
b) \(\left( {6{x^2}{y^2} - x{y^2} + 3{x^2}y} \right): - 3xy\)
Phương pháp giải:
Áp dụng quy tắc chia đa thức cho đơn thức.
Lời giải chi tiết:
a) \(\left( {5ab - 2{a^2}} \right):a\)
\( = \left( {5ab:a} \right) - \left( {2{a^2}:a} \right)\)
\( = 5b - 2a\)
b) \(\left( {6{x^2}{y^2} - x{y^2} + 3{x^2}y} \right): - 3xy\)
\( = \left[ {6{x^2}{y^2}:\left( { - 3xy} \right)} \right] - \left[ {x{y^2}:\left( { - 3xy} \right)} \right] + \left[ {3{x^2}y:\left( { - 3xy} \right)} \right]\)
\( = - 2xy - \left( { - \frac{1}{3}y} \right) + \left( { - x} \right)\)
\( = - 2xy + \frac{1}{3}y - x\)
Video hướng dẫn giải
Tính chiều cao của hình hộp chữ nhật có thể tích \(V = 6{x^2}y - 8x{y^2}\) và diện tích đáy \(S = 2xy\).
Phương pháp giải:
Áp dụng công thức tính chiều cao hình hộp chữ nhật: \(h = V:S\) trong đó \(S\), \(V\), \(h\) lần lượt là diện tích đáy, thể tích, chiều cao của hình hộp chữ nhật.
Áp dụng quy tắc chia đa thức cho đơn thức.
Lời giải chi tiết:
Chiều cao của hình hộp chữ nhật là:
\(\left( {6{x^2}y - 8x{y^2}} \right):\left( {2xy} \right) = \left[ {6{x^2}y:\left( {2xy} \right)} \right] - \left[ {8x{y^2}:\left( {2xy} \right)} \right]\)\( = 3x - 4y\)
Mục 3 trong SGK Toán 8 tập 1 – Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về đa thức, phân thức đại số. Các bài tập trong mục này giúp học sinh rèn luyện kỹ năng biến đổi đa thức, phân thức, thực hiện các phép toán cộng, trừ, nhân, chia và rút gọn biểu thức. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán.
Mục 3 trang 15, 16 bao gồm một loạt các bài tập khác nhau, từ cơ bản đến nâng cao, nhằm kiểm tra và đánh giá mức độ hiểu bài của học sinh. Các bài tập thường yêu cầu:
Bài 1 yêu cầu rút gọn biểu thức: (3x + 2)(x - 1). Để giải bài này, học sinh cần áp dụng quy tắc nhân hai đa thức: (a + b)(c + d) = ac + ad + bc + bd. Áp dụng quy tắc này, ta có:
(3x + 2)(x - 1) = 3x * x + 3x * (-1) + 2 * x + 2 * (-1) = 3x2 - 3x + 2x - 2 = 3x2 - x - 2
Bài 2 yêu cầu tìm giá trị của biểu thức: 2x2 - 5x + 3 khi x = 2. Để giải bài này, học sinh cần thay x = 2 vào biểu thức và tính toán:
2 * (2)2 - 5 * (2) + 3 = 2 * 4 - 10 + 3 = 8 - 10 + 3 = 1
Bài 3 yêu cầu giải phương trình: 3x - 6 = 0. Để giải bài này, học sinh cần chuyển vế và thực hiện các phép toán để tìm ra giá trị của x:
3x - 6 = 0 => 3x = 6 => x = 6 / 3 = 2
Toán 8 là một môn học quan trọng, đóng vai trò nền tảng cho các môn học khác trong chương trình THCS và THPT. Việc học tốt Toán 8 sẽ giúp học sinh:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập mục 3 trang 15, 16 SGK Toán 8 tập 1 – Chân trời sáng tạo, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán. Hãy luyện tập thường xuyên và áp dụng các mẹo giải bài tập hiệu quả để đạt kết quả tốt nhất.