Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 52, 53 SGK Toán 8 tập 2 – Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic, kèm theo các ví dụ minh họa cụ thể.
Cho tam giác
Video hướng dẫn giải
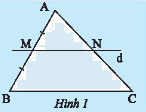
Cho tam giác \(ABC\), vẽ đường thẳng \(d\) đi qua trung điểm \(M\) của cạnh \(AB\), song song với cạnh \(BC\) và cắt \(AC\) tại \(N\) (Hình 1). Hãy chứng minh \(N\) là trung điểm của \(AC\).
Phương pháp giải:
Sử dụng định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
Xét tam giác \(ABC\) có \(MN//BC\) nên áp dụng định lí Thales cho tam giác ta có:
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\).
Mà \(M\) là trung điểm của \(AB\) nên \(AM = \frac{1}{2}BC\) hay \(\frac{{AM}}{{BC}} = \frac{1}{2}\).
Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{2}\) suy ra \( \frac{{AN}}{{AC}} = \frac{1}{2} \) nên \(AN = \frac{1}{2}AC\).
Do đó, \(N\) là trung điểm của \(AC\).
Video hướng dẫn giải
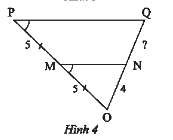
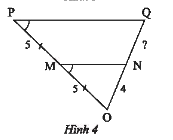
Tìm độ dài đoạn thẳng \(NQ\) trong Hình 4.
Phương pháp giải:
Sử dụng định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
Từ hình vẽ ta có: \(\widehat {OMN} = \widehat {OPQ}\).
Mà hai góc này ở vị trí đồng vị nên \(MN//PQ\)
Xét tam giác \(OPQ\) có \(MN//PQ\) nên áp dụng định lí Thales cho tam giác ta có:
\(\frac{{OM}}{{MP}} = \frac{{ON}}{{NQ}} \)
\(\frac{5}{5} = \frac{4}{{NQ}} \)
suy ra \(NQ = \frac{{4.5}}{5} = 4\).
Vậy \(NQ = 4\).
Video hướng dẫn giải
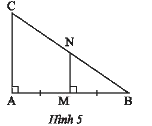
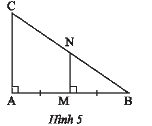
Trong Hình 5, chứng minh \(MN\) là đường trung bình của tam giác \(ABC\).
Phương pháp giải:
- Đường trung bình của tam giác là đoạn thẳng nối hai trung điểm hai cạnh tam giác.
- Hệ quả của định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết:
Vì \(\left\{ \begin{array}{l}MN \bot AB\\CA \bot AB\end{array} \right. \) nên \(MN//CA\) (Quan hệ từ vuông góc đến song song).
Ta có:
\(AM = BM \) và \(BM = \frac{1}{2}AB \) nên \(\frac{{BM}}{{AB}} = \frac{1}{2}\) hay \(M\) là trung điểm của \(AB\).
Xét tam giác \(ABC\) có \(NM//AC;MN\) cắt \(BA;BC\) lần lượt tại \(M;N\). Theo hệ quả của định lí Thales ta có:
\(\frac{{BM}}{{AB}} = \frac{{BN}}{{BC}} \)
\(\frac{{BN}}{{BC}} = \frac{1}{2}\)
Hay \(2BN = BC\). Do đó, \(N\) là trung điểm của \(BC\).
Xét tam giác \(ABC\) có:
\(M\) là trrung điểm của \(AB\)
\(N\) là trrung điểm của \(BC\)
Do đó, \(MN\) là đường trung bình của tam giác \(ABC\) (điều phải chứng minh).
Video hướng dẫn giải
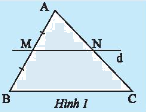
Cho tam giác \(ABC\), vẽ đường thẳng \(d\) đi qua trung điểm \(M\) của cạnh \(AB\), song song với cạnh \(BC\) và cắt \(AC\) tại \(N\) (Hình 1). Hãy chứng minh \(N\) là trung điểm của \(AC\).
Phương pháp giải:
Sử dụng định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
Xét tam giác \(ABC\) có \(MN//BC\) nên áp dụng định lí Thales cho tam giác ta có:
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\).
Mà \(M\) là trung điểm của \(AB\) nên \(AM = \frac{1}{2}BC\) hay \(\frac{{AM}}{{BC}} = \frac{1}{2}\).
Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{2}\) suy ra \( \frac{{AN}}{{AC}} = \frac{1}{2} \) nên \(AN = \frac{1}{2}AC\).
Do đó, \(N\) là trung điểm của \(AC\).
Video hướng dẫn giải
Tìm độ dài đoạn thẳng \(NQ\) trong Hình 4.
Phương pháp giải:
Sử dụng định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
Từ hình vẽ ta có: \(\widehat {OMN} = \widehat {OPQ}\).
Mà hai góc này ở vị trí đồng vị nên \(MN//PQ\)
Xét tam giác \(OPQ\) có \(MN//PQ\) nên áp dụng định lí Thales cho tam giác ta có:
\(\frac{{OM}}{{MP}} = \frac{{ON}}{{NQ}} \)
\(\frac{5}{5} = \frac{4}{{NQ}} \)
suy ra \(NQ = \frac{{4.5}}{5} = 4\).
Vậy \(NQ = 4\).
Video hướng dẫn giải
Trong Hình 5, chứng minh \(MN\) là đường trung bình của tam giác \(ABC\).
Phương pháp giải:
- Đường trung bình của tam giác là đoạn thẳng nối hai trung điểm hai cạnh tam giác.
- Hệ quả của định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết:
Vì \(\left\{ \begin{array}{l}MN \bot AB\\CA \bot AB\end{array} \right. \) nên \(MN//CA\) (Quan hệ từ vuông góc đến song song).
Ta có:
\(AM = BM \) và \(BM = \frac{1}{2}AB \) nên \(\frac{{BM}}{{AB}} = \frac{1}{2}\) hay \(M\) là trung điểm của \(AB\).
Xét tam giác \(ABC\) có \(NM//AC;MN\) cắt \(BA;BC\) lần lượt tại \(M;N\). Theo hệ quả của định lí Thales ta có:
\(\frac{{BM}}{{AB}} = \frac{{BN}}{{BC}} \)
\(\frac{{BN}}{{BC}} = \frac{1}{2}\)
Hay \(2BN = BC\). Do đó, \(N\) là trung điểm của \(BC\).
Xét tam giác \(ABC\) có:
\(M\) là trrung điểm của \(AB\)
\(N\) là trrung điểm của \(BC\)
Do đó, \(MN\) là đường trung bình của tam giác \(ABC\) (điều phải chứng minh).
Mục 1 của chương trình Toán 8 tập 2 – Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa các kiến thức về đa thức, phân thức đại số. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các quy tắc cộng, trừ, nhân, chia đa thức, phân thức để giải quyết các bài toán thực tế. Việc nắm vững kiến thức nền tảng và kỹ năng giải toán là vô cùng quan trọng để đạt kết quả tốt trong các bài kiểm tra và kỳ thi sắp tới.
Bài tập mục 1 trang 52, 53 SGK Toán 8 tập 2 – Chân trời sáng tạo bao gồm các dạng bài tập sau:
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 1 trang 52, 53 SGK Toán 8 tập 2 – Chân trời sáng tạo:
a) (3x + 2y) + (2x - y)
Lời giải: (3x + 2y) + (2x - y) = 3x + 2y + 2x - y = (3x + 2x) + (2y - y) = 5x + y
a) (x + 2)(x - 3)
Lời giải: (x + 2)(x - 3) = x(x - 3) + 2(x - 3) = x2 - 3x + 2x - 6 = x2 - x - 6
a) x2 - 4
Lời giải: x2 - 4 = (x - 2)(x + 2) (Sử dụng hằng đẳng thức a2 - b2 = (a - b)(a + b))
Kiến thức về đa thức, phân thức đại số có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học kỹ thuật. Ví dụ, trong vật lý, các công thức tính vận tốc, gia tốc, lực thường được biểu diễn dưới dạng các biểu thức đại số. Trong kinh tế, các mô hình toán học được sử dụng để phân tích và dự đoán các xu hướng thị trường.
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh đã có thể tự tin giải quyết các bài tập mục 1 trang 52, 53 SGK Toán 8 tập 2 – Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi sắp tới!