Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 89 và 90 sách giáo khoa Toán 8 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập. Hãy cùng theo dõi và tham khảo lời giải dưới đây nhé!
Gieo một con xúc xắc cân đối đồng và đồng chất. Gọi
Video hướng dẫn giải
Gieo một con xúc xắc cân đối đồng và đồng chất. Gọi \(A\) là biến cố gieo được mặt có số chấm chia hết cho 3. Tính xác suất của biến cố \(A\).
Phương pháp giải:
Khi tất cả các kết quả của một trò chơi hay phép thử ngẫu nghiệm đều có khả năng xảy ra bằng nhau thì xác suất xảy ra biến cố \(A\) là tỉ số giữ số kết quả thuận lời cho \(A\) và tổng số kết quả có thể xảy ra của phép thử, tức là:
\(P\left( A \right) = \)Số kết quả thuận lợi : Số kết quả có thể xảy ra.
Lời giải chi tiết:
Số kết quả có thể xảy ra là 6 vì con xúc xắc có 6 mặt.
Số kết quả thuận lời của \(A\) là 2 (ứng với mặt 3 chấm và mặt 6 châm).
Xác suất của biến cố \(A\) là:
\(P\left( A \right) = \frac{2}{6} = \frac{1}{3}\).
Video hướng dẫn giải
Hãy trả lời câu hỏi ở trang (88)
Một hộp có 1 quả bóng xanh và 4 quả bóng đỏ có kích thước và khối lượng như nhau. Châu lấy ra ngẫu nhiên 1 quả bóng từ hộp. Theo em, khả năng Châu lấy được bóng đỏ bằng mấy lần khả năng Châu lấy được bóng xanh.?
Phương pháp giải:
Khi tất cả các kết quả của một trò chơi hay phép thử ngẫu nghiệm đều có khả năng xảy ra bằng nhau thì xác suất xảy ra biến cố \(A\) là tỉ số giữ số kết quả thuận lời cho \(A\) và tổng số kết quả có thể xảy ra của phép thử, tức là:
\(P\left( A \right) = \) Số kết quả thuận lợi : Số kết quả có thể xảy ra.
Lời giải chi tiết:
Có tất cả 5 quả bóng nên số kết quả có thể xảy ra là 5.
Gọi \(A\) là biến cố lấy được bóng màu đỏ và \(B\) là biến cố lấy được bóng màu xanh.
Biến cố \(A\) xảy ra khi lấy được bóng màu đỏ và ở đây có 4 quả bóng màu đỏ nên số kết quả thuận lợi là 4. Xác suất của biến cố \(A\) là:
\(P\left( A \right) = \frac{4}{5}\)
Biến cố \(B\) xảy ra khi lấy được bóng màu xanh và ở đây có 1 quả bóng màu xanh nên số kết quả thuận lợi là 1. Xác suất của biến cố \(B\) là:
\(P\left( B \right) = \frac{1}{5}\)
Khả năng Châu lấy được bóng đỏ gấp số lần khả năng Châu lấy được bóng xanh là:
\(\frac{4}{5}:\frac{1}{5} = \frac{4}{1} = 4\)
Video hướng dẫn giải
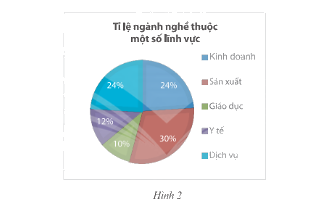
Một khu phố có 200 người lao động, mỗi người làm việc ở trong năm lĩnh vực là Kinh doanh, Sản xuất, Giáo dục, Y tế và Dịch vụ. Biểu đồ trong Hình 2 thông kê tỉ lệ người lao động thuộc mỗi lĩnh vực nghề nghiệp.
Gặp ngẫu nhiên một người lao động của khu phố.
a) Tính xác suất người đó có công việc thuộc lĩnh vực Giáo dục.
b) Tính xác suất người đó có công việc không thuộc lĩnh vực Y tế hay Dịch vụ.
Phương pháp giải:
Khi tất cả các kết quả của một trò chơi hay phép thử ngẫu nghiệm đều có khả năng xảy ra bằng nhau thì xác suất xảy ra biến cố \(A\) là tỉ số giữ số kết quả thuận lời cho \(A\) và tổng số kết quả có thể xảy ra của phép thử, tức là:
\(P\left( A \right) = \)Số kết quả thuận lợi : Số kết quả có thể xảy ra.
Lời giải chi tiết:
Vì gặp ngẫu nhiên một người trong 200 người nên 200 kết quả có khả năng xảy ra như nhau.
Số người làm Kinh doanh trong 200 người ở khu phố là:
\(200.24\% = 48\) (người)
Số người làm Y tế trong 200 người ở khu phố là:
\(200.12\% = 24\) (người)
Số người làm Giáo dục trong 200 người ở khu phố là:
\(200.10\% = 20\) (người)
Số người làm Sản xuất trong 200 người ở khu phố là:
\(200.30\% = 60\) (người)
Số người làm Dịch vụ trong 200 người ở khu phố là:
\(200.24\% = 48\) (người)
a) Gọi \(A\) là biến cố người gặp ngẫu nhiên là người làm trong lĩnh vực giáo dục.
Biến cố \(A\) xảy ra khi người gặp ngẫu nhiên là người làm trong lĩnh vực giáo dục do đó, số kết quả thuận lợi của biến cố \(A\) là 20. Xác suất của biến cố \(A\) là:
\(P\left( A \right) = \frac{{20}}{{200}} = \frac{1}{{10}}\)
b) Gọi \(B\) là biến cố người gặp ngẫu nhiên không thuộc lĩnh vực Y tế hay Dịch vụ do đó, người gặp ngẫu nhiên có thể thuộc lĩnh vực Kinh doanh, Giáo dục hoặc Sản xuất.
Biến cố \(B\) xảy ra khi người gặp ngẫu nhiên là người làm trong lĩnh vực Kinh doanh, Giáo dục hoặc Sản xuất do đó, số kết quả thuận lợi của biến cố \(B\) là: 48 + 20 + 60 = 128.
Xác suất của biến cố \(B\) là:
\(P\left( B \right) = \frac{{128}}{{200}} = \frac{{16}}{{25}}\).
Video hướng dẫn giải
Gieo một con xúc xắc cân đối đồng và đồng chất. Gọi \(A\) là biến cố gieo được mặt có số chấm chia hết cho 3. Tính xác suất của biến cố \(A\).
Phương pháp giải:
Khi tất cả các kết quả của một trò chơi hay phép thử ngẫu nghiệm đều có khả năng xảy ra bằng nhau thì xác suất xảy ra biến cố \(A\) là tỉ số giữ số kết quả thuận lời cho \(A\) và tổng số kết quả có thể xảy ra của phép thử, tức là:
\(P\left( A \right) = \)Số kết quả thuận lợi : Số kết quả có thể xảy ra.
Lời giải chi tiết:
Số kết quả có thể xảy ra là 6 vì con xúc xắc có 6 mặt.
Số kết quả thuận lời của \(A\) là 2 (ứng với mặt 3 chấm và mặt 6 châm).
Xác suất của biến cố \(A\) là:
\(P\left( A \right) = \frac{2}{6} = \frac{1}{3}\).
Video hướng dẫn giải
Hãy trả lời câu hỏi ở trang (88)
Một hộp có 1 quả bóng xanh và 4 quả bóng đỏ có kích thước và khối lượng như nhau. Châu lấy ra ngẫu nhiên 1 quả bóng từ hộp. Theo em, khả năng Châu lấy được bóng đỏ bằng mấy lần khả năng Châu lấy được bóng xanh.?
Phương pháp giải:
Khi tất cả các kết quả của một trò chơi hay phép thử ngẫu nghiệm đều có khả năng xảy ra bằng nhau thì xác suất xảy ra biến cố \(A\) là tỉ số giữ số kết quả thuận lời cho \(A\) và tổng số kết quả có thể xảy ra của phép thử, tức là:
\(P\left( A \right) = \) Số kết quả thuận lợi : Số kết quả có thể xảy ra.
Lời giải chi tiết:
Có tất cả 5 quả bóng nên số kết quả có thể xảy ra là 5.
Gọi \(A\) là biến cố lấy được bóng màu đỏ và \(B\) là biến cố lấy được bóng màu xanh.
Biến cố \(A\) xảy ra khi lấy được bóng màu đỏ và ở đây có 4 quả bóng màu đỏ nên số kết quả thuận lợi là 4. Xác suất của biến cố \(A\) là:
\(P\left( A \right) = \frac{4}{5}\)
Biến cố \(B\) xảy ra khi lấy được bóng màu xanh và ở đây có 1 quả bóng màu xanh nên số kết quả thuận lợi là 1. Xác suất của biến cố \(B\) là:
\(P\left( B \right) = \frac{1}{5}\)
Khả năng Châu lấy được bóng đỏ gấp số lần khả năng Châu lấy được bóng xanh là:
\(\frac{4}{5}:\frac{1}{5} = \frac{4}{1} = 4\)
Video hướng dẫn giải
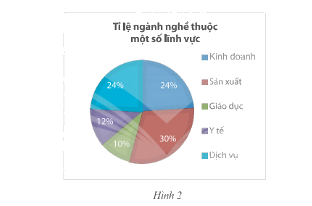
Một khu phố có 200 người lao động, mỗi người làm việc ở trong năm lĩnh vực là Kinh doanh, Sản xuất, Giáo dục, Y tế và Dịch vụ. Biểu đồ trong Hình 2 thông kê tỉ lệ người lao động thuộc mỗi lĩnh vực nghề nghiệp.
Gặp ngẫu nhiên một người lao động của khu phố.
a) Tính xác suất người đó có công việc thuộc lĩnh vực Giáo dục.
b) Tính xác suất người đó có công việc không thuộc lĩnh vực Y tế hay Dịch vụ.
Phương pháp giải:
Khi tất cả các kết quả của một trò chơi hay phép thử ngẫu nghiệm đều có khả năng xảy ra bằng nhau thì xác suất xảy ra biến cố \(A\) là tỉ số giữ số kết quả thuận lời cho \(A\) và tổng số kết quả có thể xảy ra của phép thử, tức là:
\(P\left( A \right) = \)Số kết quả thuận lợi : Số kết quả có thể xảy ra.
Lời giải chi tiết:
Vì gặp ngẫu nhiên một người trong 200 người nên 200 kết quả có khả năng xảy ra như nhau.
Số người làm Kinh doanh trong 200 người ở khu phố là:
\(200.24\% = 48\) (người)
Số người làm Y tế trong 200 người ở khu phố là:
\(200.12\% = 24\) (người)
Số người làm Giáo dục trong 200 người ở khu phố là:
\(200.10\% = 20\) (người)
Số người làm Sản xuất trong 200 người ở khu phố là:
\(200.30\% = 60\) (người)
Số người làm Dịch vụ trong 200 người ở khu phố là:
\(200.24\% = 48\) (người)
a) Gọi \(A\) là biến cố người gặp ngẫu nhiên là người làm trong lĩnh vực giáo dục.
Biến cố \(A\) xảy ra khi người gặp ngẫu nhiên là người làm trong lĩnh vực giáo dục do đó, số kết quả thuận lợi của biến cố \(A\) là 20. Xác suất của biến cố \(A\) là:
\(P\left( A \right) = \frac{{20}}{{200}} = \frac{1}{{10}}\)
b) Gọi \(B\) là biến cố người gặp ngẫu nhiên không thuộc lĩnh vực Y tế hay Dịch vụ do đó, người gặp ngẫu nhiên có thể thuộc lĩnh vực Kinh doanh, Giáo dục hoặc Sản xuất.
Biến cố \(B\) xảy ra khi người gặp ngẫu nhiên là người làm trong lĩnh vực Kinh doanh, Giáo dục hoặc Sản xuất do đó, số kết quả thuận lợi của biến cố \(B\) là: 48 + 20 + 60 = 128.
Xác suất của biến cố \(B\) là:
\(P\left( B \right) = \frac{{128}}{{200}} = \frac{{16}}{{25}}\).
Mục 2 của chương trình Toán 8 tập 2, Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về hình hộp chữ nhật và hình lập phương. Các bài tập trong trang 89 và 90 SGK Toán 8 tập 2 yêu cầu học sinh vận dụng các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của hai hình này vào giải quyết các bài toán thực tế.
Bài tập này yêu cầu học sinh tính toán các yếu tố hình học của hình hộp chữ nhật dựa trên các kích thước đã cho. Để giải bài tập này, học sinh cần nắm vững các công thức sau:
Trong đó: a, b là chiều dài và chiều rộng của đáy; h là chiều cao của hình hộp chữ nhật.
Tương tự như bài 1, bài tập này yêu cầu học sinh tính toán các yếu tố hình học của hình lập phương. Tuy nhiên, hình lập phương có các cạnh bằng nhau, do đó công thức tính toán sẽ đơn giản hơn:
Trong đó: a là độ dài cạnh của hình lập phương.
Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán có tính ứng dụng cao trong đời sống. Ví dụ, tính lượng sơn cần thiết để sơn một căn phòng hình hộp chữ nhật, hoặc tính thể tích của một thùng hàng hình lập phương.
Để giúp các em hiểu rõ hơn về cách giải các bài tập trong mục 2 trang 89, 90 SGK Toán 8 tập 2, chúng tôi sẽ cung cấp lời giải chi tiết cho từng bài tập. Các lời giải này sẽ được trình bày một cách rõ ràng, dễ hiểu, kèm theo các bước giải cụ thể và các lưu ý quan trọng.
Ví dụ: Giải bài 1a (trang 89 SGK Toán 8 tập 2)
Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 4cm và chiều cao 3cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật đó.
Lời giải:
Diện tích xung quanh của hình hộp chữ nhật là: 2(5 + 4) x 3 = 54 cm2
Diện tích toàn phần của hình hộp chữ nhật là: 2(5 x 4 + 5 x 3 + 4 x 3) = 94 cm2
Thể tích của hình hộp chữ nhật là: 5 x 4 x 3 = 60 cm3
Ngoài SGK Toán 8 tập 2, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải toán:
Hy vọng rằng với những hướng dẫn chi tiết và lời giải cụ thể trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 2 trang 89, 90 SGK Toán 8 tập 2 – Chân trời sáng tạo. Chúc các em học tập tốt!