Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 62, 63 sách giáo khoa Toán 8 tập 2 – Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Nêu nhận xét về hình dạng và kích thước của từng cặp hình:
Video hướng dẫn giải
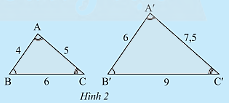
Cho tam giác \(ABC\) và tam giác \(A'B'C'\) như Hình 2.
a) Hãy viết các cặp góc bằng nhau.
b) Tính và so sánh các tỉ số
\(\frac{{A'B'}}{{AB}};\frac{{A'C'}}{{AC}};\frac{{B'C'}}{{BC}}\).
Phương pháp giải:
Quan sát, so sánh, tính tỉ số.
Lời giải chi tiết:
a) Từ kí hiệu của hình vẽ ta thấy các cặp góc bằng nhau là:
\(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
b) Ta có:
\(\frac{{A'B'}}{{AB}} = \frac{6}{4} = \frac{3}{2};\frac{{A'C'}}{{AC}} = \frac{{7,5}}{5} = \frac{3}{2};\frac{{B'C'}}{{BC}} = \frac{9}{6} = \frac{3}{2}\).
Ta thấy, \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{3}{2}\)
Video hướng dẫn giải
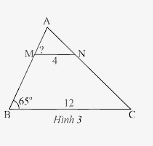
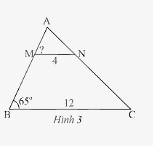
Quan sát Hình 3, cho biết \(\Delta AMN\backsim\Delta ABC\).
a) Hãy viết tỉ số của các cạnh tương ứng và tính tỉ số đồng dạng.
b) Tính góc \(\widehat {AMN}\).
Phương pháp giải:
Hai tam giác đồng dạng với nhau thì các góc tương ứng bằng nhau và các cặp cạnh tương ứng có cùng tỉ lệ.
Lời giải chi tiết:
a) Vì tam giác \(\Delta AMN\backsim\Delta ABC\) nên ta có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (các cạnh tương ứng)
Tỉ số đồng dạng là: \(\frac{{MN}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\).
b) Vì \(\Delta AMN\backsim\Delta ABC\) nên \(\widehat {AMN} = \widehat {ABC} = 65^\circ \)
Vậy \(\widehat {AMN} = 65^\circ \).
Video hướng dẫn giải
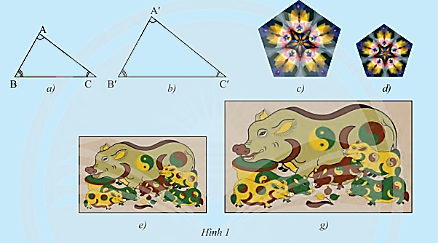
Nêu nhận xét về hình dạng và kích thước của từng cặp hình: Hình 1a và Hình 1b, Hình 1c và Hình 1d, Hình 1e và Hình 1g.

Phương pháp giải:
Quan sát và so sánh
Lời giải chi tiết:
Hình 1a và Hình 1b có kích thước không bằng nhau. Tuy nhiên ta có thể phóng to Hình 1a để thu được Hình 1b hoặc thu nhỏ Hình 1b để được Hình 1a.
Hình 1c và Hình 1d có kích thước không bằng nhau. Tuy nhiên ta có thể phóng to Hình 1d để thu được Hình 1c hoặc thu nhỏ Hình 1c để được Hình 1d.
Hình 1e và Hình 1g có kích thước không bằng nhau. Tuy nhiên ta có thể phóng to Hình 1e để thu được Hình 1g hoặc thu nhỏ Hình 1g để được Hình 1e.
Video hướng dẫn giải
Nêu nhận xét về hình dạng và kích thước của từng cặp hình: Hình 1a và Hình 1b, Hình 1c và Hình 1d, Hình 1e và Hình 1g.
Phương pháp giải:
Quan sát và so sánh
Lời giải chi tiết:
Hình 1a và Hình 1b có kích thước không bằng nhau. Tuy nhiên ta có thể phóng to Hình 1a để thu được Hình 1b hoặc thu nhỏ Hình 1b để được Hình 1a.
Hình 1c và Hình 1d có kích thước không bằng nhau. Tuy nhiên ta có thể phóng to Hình 1d để thu được Hình 1c hoặc thu nhỏ Hình 1c để được Hình 1d.
Hình 1e và Hình 1g có kích thước không bằng nhau. Tuy nhiên ta có thể phóng to Hình 1e để thu được Hình 1g hoặc thu nhỏ Hình 1g để được Hình 1e.
Video hướng dẫn giải
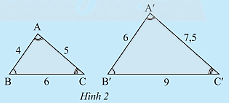
Cho tam giác \(ABC\) và tam giác \(A'B'C'\) như Hình 2.
a) Hãy viết các cặp góc bằng nhau.
b) Tính và so sánh các tỉ số
\(\frac{{A'B'}}{{AB}};\frac{{A'C'}}{{AC}};\frac{{B'C'}}{{BC}}\).
Phương pháp giải:
Quan sát, so sánh, tính tỉ số.
Lời giải chi tiết:
a) Từ kí hiệu của hình vẽ ta thấy các cặp góc bằng nhau là:
\(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
b) Ta có:
\(\frac{{A'B'}}{{AB}} = \frac{6}{4} = \frac{3}{2};\frac{{A'C'}}{{AC}} = \frac{{7,5}}{5} = \frac{3}{2};\frac{{B'C'}}{{BC}} = \frac{9}{6} = \frac{3}{2}\).
Ta thấy, \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{3}{2}\)
Video hướng dẫn giải
Quan sát Hình 3, cho biết \(\Delta AMN\backsim\Delta ABC\).
a) Hãy viết tỉ số của các cạnh tương ứng và tính tỉ số đồng dạng.
b) Tính góc \(\widehat {AMN}\).
Phương pháp giải:
Hai tam giác đồng dạng với nhau thì các góc tương ứng bằng nhau và các cặp cạnh tương ứng có cùng tỉ lệ.
Lời giải chi tiết:
a) Vì tam giác \(\Delta AMN\backsim\Delta ABC\) nên ta có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (các cạnh tương ứng)
Tỉ số đồng dạng là: \(\frac{{MN}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\).
b) Vì \(\Delta AMN\backsim\Delta ABC\) nên \(\widehat {AMN} = \widehat {ABC} = 65^\circ \)
Vậy \(\widehat {AMN} = 65^\circ \).
Mục 1 của chương trình Toán 8 tập 2 – Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa các kiến thức về tứ giác. Các bài tập trong mục này yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán thực tế liên quan đến tứ giác, đặc biệt là hình thang cân.
Bài 1 yêu cầu học sinh nhắc lại các định nghĩa, tính chất của các loại tứ giác đã học (hình vuông, hình chữ nhật, hình thoi, hình bình hành, hình thang). Đồng thời, học sinh cần biết cách áp dụng các tính chất này để chứng minh một tứ giác là một loại tứ giác cụ thể.
Ví dụ, để chứng minh một tứ giác là hình bình hành, ta có thể chứng minh một trong các điều kiện sau:
Bài 2 tập trung vào việc ôn tập về hình thang cân, bao gồm các tính chất đặc trưng như:
Các bài tập trong bài 2 thường yêu cầu học sinh tính độ dài các cạnh, góc, đường chéo của hình thang cân, hoặc chứng minh một tứ giác là hình thang cân.
Bài 3 là phần vận dụng các kiến thức đã học vào giải quyết các bài toán thực tế. Các bài toán này thường có tính ứng dụng cao, giúp học sinh hiểu rõ hơn về vai trò của tứ giác trong đời sống.
Ví dụ, một bài toán có thể yêu cầu tính chiều cao của một ngọn núi dựa vào số liệu về góc nhìn và khoảng cách từ một điểm quan sát đến chân núi, trong đó ngọn núi được xem như một hình thang cân.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 62, 63 SGK Toán 8 tập 2 – Chân trời sáng tạo:
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Lời giải chi tiết bài 1) |
| Bài 2 | (Lời giải chi tiết bài 2) |
| Bài 3 | (Lời giải chi tiết bài 3) |
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 8. Chúc các em học tốt!