Bài 12 trang 29 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, đầy đủ và dễ tiếp cận nhất, giúp các em học sinh tự tin hơn trong quá trình học tập môn Toán.
Vẽ một hệ trục tọa độ (Oxy) và đánh dấu các điểm
Đề bài
Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm \(A\left( { - 2;0} \right);B\left( {0;4} \right);C\left( {5;4} \right);D\left( {3;0} \right)\). Tứ giác \(ABCD\) là hình gì?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Điểm \(M\left( {{x_0};{y_0}} \right)\) nghĩa là hoành độ của điểm \(M\) là \({x_0}\) và tung độ của điểm \(M\) là \({y_0}\).
- Hai điểm có cùng tung độ thì đoạn thẳng nối hai điểm đó song song với trục hoành.
- Hai điểm có cùng tung độ thì độ dài đoạn thẳng nối hai điểm đó bằng giá trị tuyệt đối của hiệu hai hoành độ.
Lời giải chi tiết
\(A\left( { - 2;0} \right)\) \( \Rightarrow \) hoành độ của điểm \(A\) là –2 và tung độ của điểm \(A\) là 0.
\(B\left( {0;4} \right)\) \( \Rightarrow \) hoành độ của điểm \(B\) là 0 và tung độ của điểm \(B\) là 4.
\(C\left( {5;4} \right)\) \( \Rightarrow \) hoành độ của điểm \(C\) là 5 và tung độ của điểm \(C\) là 4.
\(D\left( {3;0} \right)\) \( \Rightarrow \) hoành độ của điểm \(D\) là 3 và tung độ của điểm \(D\) là 0.
Biểu diễn các điểm \(A;B;C;D\) trên mặt phẳng tọa độ ta được:
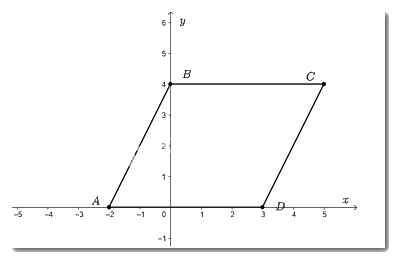
Vì hai điểm \(B;C\) có tung độ bằng nhau nên \(BC\) song song với \(Ox\); Hai điểm \(A;D\) có tung độ bằng nhau nên \(AD\) song song với \(Ox\).
Do đó, \(BC//AD\).
Lại có, \(AD = \left| {3 - \left( { - 2} \right)} \right| = 5;BC = \left| {5 - 0} \right| = 5\). Do đó, \(AD = BC\).
Xét tứ giác \(ABCD\)có:
\(AD = BC\)
\(BC//AD\)
Do đó, tứ giác \(ABCD\) là hình bình hành.
Bài 12 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về các phép biến đổi đại số, cụ thể là các phép cộng, trừ, nhân, chia đa thức để rút gọn biểu thức và tìm giá trị của biểu thức. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về dấu ngoặc, quy tắc chuyển vế, và các tính chất của phép toán.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 12, học sinh cần xác định biểu thức cần rút gọn hoặc tìm giá trị, và các dữ kiện đã cho trong đề bài.
Để giải bài 12 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo, chúng ta có thể áp dụng các bước sau:
Giả sử đề bài yêu cầu rút gọn biểu thức: (2x + 3)(x - 1) - (x + 2)(x - 3)
Chúng ta sẽ thực hiện như sau:
(2x + 3)(x - 1) = 2x2 - 2x + 3x - 3 = 2x2 + x - 3(x + 2)(x - 3) = x2 - 3x + 2x - 6 = x2 - x - 6(2x2 + x - 3) - (x2 - x - 6) = 2x2 + x - 3 - x2 + x + 6 = x2 + 2x + 3Vậy, biểu thức được rút gọn là x2 + 2x + 3
Để củng cố kiến thức và kỹ năng giải bài tập về các phép biến đổi đại số, học sinh nên luyện tập thêm với các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi giải các bài tập khó hơn.
Ngoài bài 12 trang 29, SGK Toán 8 tập 2 – Chân trời sáng tạo còn có nhiều bài tập khác liên quan đến các phép biến đổi đại số. Một số dạng bài tập tương tự bao gồm:
Khi giải bài tập về các phép biến đổi đại số, học sinh nên:
Bài 12 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bằng cách nắm vững lý thuyết, phương pháp giải và luyện tập thường xuyên, học sinh có thể tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.