Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 68, 69 SGK Toán 8 tập 2 – Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải đầy đủ, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em học sinh học tập hiệu quả và đạt kết quả tốt nhất.
Cho tam giác
Video hướng dẫn giải
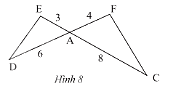
Cho tam giác \(ADE\) và tam giác \(ACF\) có các kích thước như trong Hình 8. Chứng minh rằng \(\Delta ADE\backsim\Delta ACF\).
Phương pháp giải:
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
Ta có: \(\frac{{AE}}{{AF}} = \frac{3}{4};\frac{{AD}}{{AC}} = \frac{6}{8} = \frac{3}{4}\);
Xét \(\Delta ADE\) và \(\Delta ACF\) có:
\(\frac{{AE}}{{AF}} = \frac{{AD}}{{AC}} = \frac{3}{4}\)
\(\widehat {EAD} = \widehat {FAC}\) (hai góc đối đỉnh)
Do đó, \(\Delta ADE\backsim\Delta ACF\)(c.g.c)
Video hướng dẫn giải
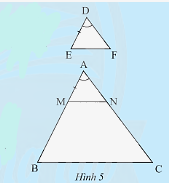
Cho tam giác \(DEF\) và tam giác \(ABC\) có \(DE = \frac{1}{3}AB,DF = \frac{1}{3}AC,\widehat D = \widehat A\) (Hình 5). Trên tia \(AB\), lấy điểm \(M\) sao cho \(AM = DE\). Qua \(M\) kẻ \(MN//BC\left( {N \in AC} \right)\).
a) So sánh \(\frac{{AM}}{{AB}}\) và \(\frac{{AN}}{{AC}}\)
b) So sánh \(AN\) với \(DF\).
c) Tam giác \(AMN\) có đồng dạng với tam giác \(ABC\) không?
d) Dự đoán sự đồng dạng của hai tam giác \(DEF\) và \(ABC\).
Phương pháp giải:
- Sử dụng định lí Thales.
- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết:
a) Vì \(MN//BC\left( {M \in AB,N \in AC} \right)\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)(định lí Thales).
b) Vì \(AM = DE\) mà \(\frac{{DE}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3} \Rightarrow AN = \frac{1}{3}AC\).
Lại có \(DF = \frac{1}{3}AC\) nên \(AN = DF = \frac{1}{3}AC\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
d) Dự đoán hai tam giác \(DEF\) và \(ABC\) đồng dạng.
Video hướng dẫn giải
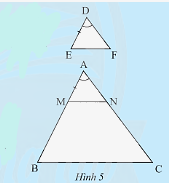
Cho tam giác \(DEF\) và tam giác \(ABC\) có \(DE = \frac{1}{3}AB,DF = \frac{1}{3}AC,\widehat D = \widehat A\) (Hình 5). Trên tia \(AB\), lấy điểm \(M\) sao cho \(AM = DE\). Qua \(M\) kẻ \(MN//BC\left( {N \in AC} \right)\).
a) So sánh \(\frac{{AM}}{{AB}}\) và \(\frac{{AN}}{{AC}}\)
b) So sánh \(AN\) với \(DF\).
c) Tam giác \(AMN\) có đồng dạng với tam giác \(ABC\) không?
d) Dự đoán sự đồng dạng của hai tam giác \(DEF\) và \(ABC\).
Phương pháp giải:
- Sử dụng định lí Thales.
- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết:
a) Vì \(MN//BC\left( {M \in AB,N \in AC} \right)\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)(định lí Thales).
b) Vì \(AM = DE\) mà \(\frac{{DE}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3} \Rightarrow AN = \frac{1}{3}AC\).
Lại có \(DF = \frac{1}{3}AC\) nên \(AN = DF = \frac{1}{3}AC\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
d) Dự đoán hai tam giác \(DEF\) và \(ABC\) đồng dạng.
Video hướng dẫn giải
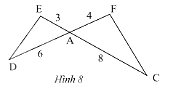
Cho tam giác \(ADE\) và tam giác \(ACF\) có các kích thước như trong Hình 8. Chứng minh rằng \(\Delta ADE\backsim\Delta ACF\).
Phương pháp giải:
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
Ta có: \(\frac{{AE}}{{AF}} = \frac{3}{4};\frac{{AD}}{{AC}} = \frac{6}{8} = \frac{3}{4}\);
Xét \(\Delta ADE\) và \(\Delta ACF\) có:
\(\frac{{AE}}{{AF}} = \frac{{AD}}{{AC}} = \frac{3}{4}\)
\(\widehat {EAD} = \widehat {FAC}\) (hai góc đối đỉnh)
Do đó, \(\Delta ADE\backsim\Delta ACF\)(c.g.c)
Mục 2 của chương trình Toán 8 tập 2 – Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về hình học, đặc biệt là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh nhắc lại các định nghĩa, tính chất của hình bình hành, cách chứng minh một tứ giác là hình bình hành. Đồng thời, học sinh cần vận dụng các kiến thức này để giải các bài toán liên quan đến tính độ dài cạnh, số đo góc, diện tích của hình bình hành.
Bài tập này tập trung vào việc ôn tập các tính chất của hình chữ nhật, mối quan hệ giữa đường chéo và các cạnh của hình chữ nhật. Học sinh cần giải các bài toán liên quan đến tính độ dài đường chéo, diện tích của hình chữ nhật, và chứng minh một tứ giác là hình chữ nhật.
Bài tập này yêu cầu học sinh ôn tập các tính chất của hình thoi, mối quan hệ giữa đường chéo và các cạnh của hình thoi. Học sinh cần giải các bài toán liên quan đến tính độ dài đường chéo, diện tích của hình thoi, và chứng minh một tứ giác là hình thoi.
Bài tập này tập trung vào việc ôn tập các tính chất của hình vuông, mối quan hệ giữa đường chéo và các cạnh của hình vuông. Học sinh cần giải các bài toán liên quan đến tính độ dài đường chéo, diện tích của hình vuông, và chứng minh một tứ giác là hình vuông.
Bài tập: Cho hình bình hành ABCD, có góc A = 60 độ, AB = 4cm, AD = 3cm. Tính diện tích hình bình hành ABCD.
Lời giải:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 8 tập 2 – Chân trời sáng tạo, hoặc tìm kiếm trên các trang web học toán online uy tín.
Hy vọng với bài giải chi tiết và những hướng dẫn trên, các em học sinh đã nắm vững kiến thức và tự tin giải các bài tập trong mục 2 trang 68, 69 SGK Toán 8 tập 2 – Chân trời sáng tạo. Chúc các em học tập tốt!