Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 1 – Chân trời sáng tạo. Mục 3 trang 20, 21 là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các phép toán và ứng dụng vào giải bài tập.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, vì vậy đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải đáp này, giúp bạn tự tin chinh phục môn Toán.
Hoàn thành các phép nhân đa thức sau vào vở, thu gọn kết quả nhận được:
Video hướng dẫn giải
Hoàn thành các phép nhân đa thức sau vào vở, thu gọn kết quả nhận được:
\(\begin{array}{l}{\left( {a + b} \right)^3} = \left( {a + b} \right){\left( {a + b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\;\; = ...\end{array}\) \(\begin{array}{l}{\left( {a - b} \right)^3} = \left( {a - b} \right){\left( {a - b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\;\; = ...\end{array}\)
Phương pháp giải:
Áp dụng hằng đẳng thức: Bình phương của một tổng, một hiệu và quy tắc nhân đa thức.
Lời giải chi tiết:
\(\begin{array}{l}{\left( {a + b} \right)^3} = \left( {a + b} \right){\left( {a + b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {{a^2} + 2ab + {b^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\; = a.{a^2} + a.2ab + a.{b^2} + b.{a^2} + b.2ab + b.{b^2}\\\;\;\;\;\;\;\;\;\;\;\; = {a^3} + 2{a^2}b + a{b^2} + {a^2}b + 2a{b^2} + {b^3}\\\;\;\;\;\;\;\;\;\;\;\; = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\end{array}\) \(\begin{array}{l}{\left( {a - b} \right)^3} = \left( {a - b} \right){\left( {a - b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {{a^2} - 2ab + {b^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\; = a.{a^2} - a.2ab + a.{b^2} - b.{a^2} + b.2ab - b.{b^2}\\\;\;\;\;\;\;\;\;\;\;\; = {a^3} - 2{a^2}b + a{b^2} - {a^2}b + 2a{b^2} - {b^3}\\\;\;\;\;\;\;\;\;\;\;\; = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\end{array}\)
Video hướng dẫn giải
Tính:
a) \({\left( {x + 2y} \right)^3}\)
b) \({\left( {3y - 1} \right)^3}\)
Phương pháp giải:
Áp dụng hằng đẳng thức: Lập phương của một tổng, một hiệu
Lời giải chi tiết:
a) \({\left( {x + 2y} \right)^3} = {x^3} + 3.{x^2}.2y + 3.x.{\left( {2y} \right)^2} + {\left( {2y} \right)^3} = {x^3} + 6{x^2}y + 12x{y^2} + 8{y^3}\)
b) \({\left( {3y - 1} \right)^3} = {\left( {3y} \right)^3} - 3.{\left( {3y} \right)^2}.1 + 3.3y{.1^2} - {1^3} = 27{y^3} - 27{y^2} + 9y - 1\)
Video hướng dẫn giải
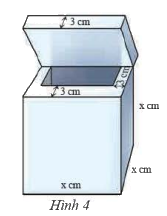
Một thùng chứa dạng hình lập phương có độ dài cạnh bằng \(x\) (cm). Phần vỏ bao gồm nắp có độ dày \(3\)cm. Tính dung tích (sức chứa) của thùng, viết kết quả dưới dạng đa thức.
Phương pháp giải:
Áp dụng công thức tính thể tích của hình lập phương.
Áp dụng hằng đẳng thức: Lập phương của một hiệu.
Lời giải chi tiết:
Dung tích của thùng có độ dài các cạnh là: \(x - 3 - 3 = x - 6(cm)\)
Dung tích (sức chứa) của thùng là:
\((x - 6)^3 = x^3 - 18x^2 + 108x - 216(cm^3)\)
Video hướng dẫn giải
Hoàn thành các phép nhân đa thức sau vào vở, thu gọn kết quả nhận được:
\(\begin{array}{l}{\left( {a + b} \right)^3} = \left( {a + b} \right){\left( {a + b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\;\; = ...\end{array}\) \(\begin{array}{l}{\left( {a - b} \right)^3} = \left( {a - b} \right){\left( {a - b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\;\; = ...\end{array}\)
Phương pháp giải:
Áp dụng hằng đẳng thức: Bình phương của một tổng, một hiệu và quy tắc nhân đa thức.
Lời giải chi tiết:
\(\begin{array}{l}{\left( {a + b} \right)^3} = \left( {a + b} \right){\left( {a + b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {{a^2} + 2ab + {b^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\; = a.{a^2} + a.2ab + a.{b^2} + b.{a^2} + b.2ab + b.{b^2}\\\;\;\;\;\;\;\;\;\;\;\; = {a^3} + 2{a^2}b + a{b^2} + {a^2}b + 2a{b^2} + {b^3}\\\;\;\;\;\;\;\;\;\;\;\; = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\end{array}\) \(\begin{array}{l}{\left( {a - b} \right)^3} = \left( {a - b} \right){\left( {a - b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {{a^2} - 2ab + {b^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\; = a.{a^2} - a.2ab + a.{b^2} - b.{a^2} + b.2ab - b.{b^2}\\\;\;\;\;\;\;\;\;\;\;\; = {a^3} - 2{a^2}b + a{b^2} - {a^2}b + 2a{b^2} - {b^3}\\\;\;\;\;\;\;\;\;\;\;\; = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\end{array}\)
Video hướng dẫn giải
Tính:
a) \({\left( {x + 2y} \right)^3}\)
b) \({\left( {3y - 1} \right)^3}\)
Phương pháp giải:
Áp dụng hằng đẳng thức: Lập phương của một tổng, một hiệu
Lời giải chi tiết:
a) \({\left( {x + 2y} \right)^3} = {x^3} + 3.{x^2}.2y + 3.x.{\left( {2y} \right)^2} + {\left( {2y} \right)^3} = {x^3} + 6{x^2}y + 12x{y^2} + 8{y^3}\)
b) \({\left( {3y - 1} \right)^3} = {\left( {3y} \right)^3} - 3.{\left( {3y} \right)^2}.1 + 3.3y{.1^2} - {1^3} = 27{y^3} - 27{y^2} + 9y - 1\)
Video hướng dẫn giải
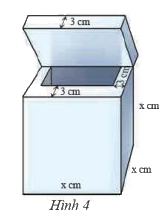
Một thùng chứa dạng hình lập phương có độ dài cạnh bằng \(x\) (cm). Phần vỏ bao gồm nắp có độ dày \(3\)cm. Tính dung tích (sức chứa) của thùng, viết kết quả dưới dạng đa thức.
Phương pháp giải:
Áp dụng công thức tính thể tích của hình lập phương.
Áp dụng hằng đẳng thức: Lập phương của một hiệu.
Lời giải chi tiết:
Dung tích của thùng có độ dài các cạnh là: \(x - 3 - 3 = x - 6(cm)\)
Dung tích (sức chứa) của thùng là:
\((x - 6)^3 = x^3 - 18x^2 + 108x - 216(cm^3)\)
Mục 3 trong SGK Toán 8 tập 1 – Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức cơ bản về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ, và các tính chất của các phép toán này. Việc nắm vững những kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 8.
Dưới đây là giải chi tiết từng bài tập trong mục 3 trang 20, 21 SGK Toán 8 tập 1 – Chân trời sáng tạo:
a) 1/2 + 1/3
Lời giải: Để cộng hai phân số, ta quy đồng mẫu số. Mẫu số chung nhỏ nhất của 2 và 3 là 6. Ta có:
1/2 + 1/3 = 3/6 + 2/6 = 5/6
b) 2/5 - 1/4
Lời giải: Tương tự như trên, ta quy đồng mẫu số. Mẫu số chung nhỏ nhất của 5 và 4 là 20. Ta có:
2/5 - 1/4 = 8/20 - 5/20 = 3/20
c) 3/4 * 2/7
Lời giải: Để nhân hai phân số, ta nhân tử số với tử số và mẫu số với mẫu số.
3/4 * 2/7 = (3 * 2) / (4 * 7) = 6/28 = 3/14
d) 5/6 : 1/2
Lời giải: Để chia hai phân số, ta nhân phân số thứ nhất với nghịch đảo của phân số thứ hai.
5/6 : 1/2 = 5/6 * 2/1 = 10/6 = 5/3
a) x + 1/2 = 3/4
Lời giải: Để tìm x, ta trừ cả hai vế của phương trình cho 1/2.
x = 3/4 - 1/2 = 3/4 - 2/4 = 1/4
b) x - 2/3 = 1/5
Lời giải: Để tìm x, ta cộng cả hai vế của phương trình cho 2/3.
x = 1/5 + 2/3 = 3/15 + 10/15 = 13/15
a) 1/2 + 2/3 + 3/4
Lời giải: Quy đồng mẫu số chung là 12.
1/2 + 2/3 + 3/4 = 6/12 + 8/12 + 9/12 = 23/12
Hy vọng với bộ giải chi tiết này, các bạn học sinh sẽ tự tin hơn trong việc giải các bài tập Toán 8 tập 1 – Chân trời sáng tạo. Chúc các bạn học tốt và đạt kết quả cao!