Bài 11 trang 85 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về ứng dụng thực tế của phương trình bậc nhất một ẩn. Bài tập này thường yêu cầu học sinh xây dựng phương trình để mô tả một tình huống cụ thể và giải phương trình đó để tìm ra nghiệm.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 11 trang 85 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
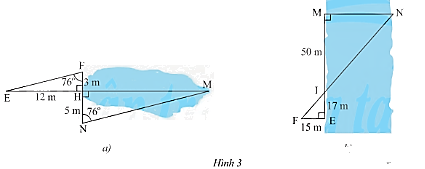
a) Tính khoảng cách
Đề bài
a) Tính khoảng cách \(HM\) của mặt hồ ở Hình 3a.
b) Tính khoảng cách \(MN\) của một khúc sông ở Hình 3b.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
- Nếu \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = k\)
Lời giải chi tiết
a) Xét tam giác \(EFH\) và tam giác \(MNH\) có:
\(\widehat {EFH} = \widehat {MNH} = 76^\circ \) (giả thuyết)
\(\widehat {EHF} = \widehat {NHM} = 90^\circ \) (giải thuyết)
Suy ra, \(\Delta EFH\backsim\Delta MNH\) (g.g)
Suy ra, \(\frac{{EH}}{{MH}} = \frac{{FH}}{{NH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{12}}{{MH}} = \frac{3}{5} \Rightarrow MH = 12.5:3 = 20\).
Vậy khoảng cách \(HM\) của mặt hồ là 20m.
b) Xét tam giác \(MNI\) và tam giác \(EFI\) có:
\(\widehat {MIN} = \widehat {EIF}\) (hai góc đối đỉnh)
\(\widehat {NMI} = \widehat {FEI} = 90^\circ \) (giải thuyết)
Suy ra, \(\Delta MNI\backsim\Delta EFI\) (g.g)
Suy ra, \(\frac{{MI}}{{EI}} = \frac{{MN}}{{EF}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{50}}{{17}} = \frac{{MN}}{{15}} \Rightarrow MN = 50.15:17 = \frac{{750}}{{17}}\).
Vậy khoảng cách \(MN\) của mặt hồ là sấp sỉ 44m.
Bài 11 trang 85 SGK Toán 8 tập 2 Chân trời sáng tạo yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính toán chi phí và lợi nhuận. Bài toán thường mô tả một tình huống kinh doanh đơn giản, trong đó học sinh cần xác định số lượng sản phẩm cần bán để đạt được một mức lợi nhuận nhất định.
Đề bài: Một người bán hàng bỏ ra 800 000 đồng để mua một số lượng táo. Người đó định bán mỗi quả táo với giá 5 000 đồng. Hỏi người đó cần bán bao nhiêu quả táo để thu được lợi nhuận 200 000 đồng?
Giải:
Ta có phương trình: 5000x - 800 000 = 200 000
Giải phương trình:
5000x = 1 000 000
x = 200
Kết luận: Người đó cần bán 200 quả táo để thu được lợi nhuận 200 000 đồng.
Để củng cố kiến thức và kỹ năng giải bài toán ứng dụng phương trình bậc nhất một ẩn, các em học sinh có thể tự giải các bài tập tương tự sau:
Giaitoan.edu.vn là một website học Toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết cho các môn Toán từ lớp 6 đến lớp 12. Với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại, Giaitoan.edu.vn sẽ giúp các em học sinh học Toán một cách hiệu quả và đạt kết quả cao.
| Công thức | Mô tả |
|---|---|
| Tổng doanh thu = Giá bán x Số lượng bán | Tính tổng số tiền thu được từ việc bán hàng. |
| Lợi nhuận = Tổng doanh thu - Tổng chi phí | Tính số tiền lãi thu được sau khi trừ đi các chi phí. |