Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho bài 1 trang 69, 70 Vở thực hành Toán 9 tập 2. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán học.
Chúng tôi hiểu rằng việc giải bài tập Toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách cẩn thận, kèm theo các bước giải thích rõ ràng, giúp các em hiểu được bản chất của vấn đề.
Chọn ngẫu nhiên một gia đình có hai con và quan sát giới tính của hai người con đó. a) Phép thử và kết quả của phép thử là gì? b) Mô tả không gian mẫu của phép thử.
Đề bài
Chọn ngẫu nhiên một gia đình có hai con và quan sát giới tính của hai người con đó.
a) Phép thử và kết quả của phép thử là gì?
b) Mô tả không gian mẫu của phép thử.
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về phép thử để tìm phép thử: Một hoặc một số hành động, thực nghiệm được tiến hành liên tiếp hay đồng thời mà kết quả của chúng không thể biết được trước khi thực hiện nhưng có thể liệt kê các kết quả có thể xảy ra, được gọi là một phép thử ngẫu nhiên, gọi tắt là phép thử.
b) Sử dụng kiến thức về không gian mẫu để tìm không gian mẫu: Sử dụng kiến thức về không gian mẫu để tìm không gian mẫu: Tập hợp tất cả các kết quả có thể xảy ra của phép thử (gọi tắt là tập tất cả các kết quả có thể của phép thử) được gọi là không gian mẫu của phép thử.
Lời giải chi tiết
a) Phép thử là quan sát giới tính của hai người con trong một gia đình.
Kết quả của phép thử là có dạng ab trong đó, a, b là lần lượt là giới tính của người con cả và người thứ trong gia đình.
b) Kí hiệu T, G tương ứng là con trai và con gái. Ta lập bảng sau:
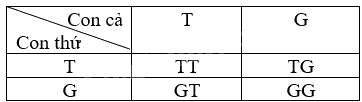
Không gian mẫu của phép thử là $\Omega =${ TT; TG; GT; GG}. Không gian mẫu có 4 phần tử.
Bài 1 trang 69, 70 Vở thực hành Toán 9 tập 2 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 bao gồm một số câu hỏi và bài tập nhỏ, yêu cầu học sinh:
Câu a: Cho hàm số y = 2x - 3. Xác định hệ số a và b.
Giải:
Hàm số y = 2x - 3 có dạng y = ax + b, trong đó a = 2 và b = -3.
Câu b: Vẽ đồ thị của hàm số y = 2x - 3.
Giải:
Để vẽ đồ thị của hàm số y = 2x - 3, ta cần xác định hai điểm thuộc đồ thị. Ví dụ, ta có thể chọn x = 0 và x = 1:
Nối hai điểm A và B, ta được đồ thị của hàm số y = 2x - 3.
Câu a: Cho hàm số y = -x + 1. Tìm tọa độ giao điểm của đồ thị với trục hoành.
Giải:
Giao điểm của đồ thị với trục hoành là điểm có tung độ y = 0. Thay y = 0 vào phương trình hàm số, ta được:
0 = -x + 1 => x = 1
Vậy tọa độ giao điểm của đồ thị với trục hoành là (1; 0).
Câu b: Giải bài toán ứng dụng: Một người đi xe đạp với vận tốc 15km/h. Hỏi sau 2 giờ người đó đi được bao nhiêu km?
Giải:
Gọi x là thời gian đi (giờ) và y là quãng đường đi được (km). Ta có hàm số y = 15x.
Khi x = 2, y = 15(2) = 30.
Vậy sau 2 giờ người đó đi được 30 km.
Ngoài Vở thực hành Toán 9 tập 2, các em có thể tham khảo thêm:
Hy vọng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải bài 1 trang 69, 70 Vở thực hành Toán 9 tập 2 một cách hiệu quả. Chúc các em học tập tốt!