Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 9. Chúng tôi hiểu rằng việc giải các bài tập trắc nghiệm trong Vở thực hành Toán 9 có thể gặp nhiều khó khăn.
Do đó, chúng tôi đã biên soạn bộ giải đáp đầy đủ, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho tam giác ABC có (widehat A = {90^o}) (H 4.2). A. (sin B = frac{{AB}}{{BC}}). B. (cos C = frac{{AC}}{{AB}}). C. (tan B = frac{{AC}}{{AB}}). D. (cot C = frac{{AB}}{{BC}}).
Trả lời Câu 4 trang 72 Vở thực hành Toán 9
A. \(\sin {82^o} = - \cos {8^o}\).
B. \(\cos {75^o} = \sin {16^o}\).
C. \(\cot {52^o} = - \tan {28^o}\).
D. \(\tan {30^o}40' = \cot {59^o}20'\).
Phương pháp giải:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Lời giải chi tiết:
Vì \({30^o}40' + {59^o}20' = {90^o}\) nên \(\tan {30^o}40' = \cot {59^o}20'\)
Chọn D
Trả lời Câu 1 trang 72 Vở thực hành Toán 9
Cho tam giác ABC có \(\widehat A = {90^o}\) (H 4.2).
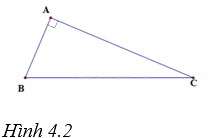
A. \(\sin B = \frac{{AB}}{{BC}}\).
B. \(\cos C = \frac{{AC}}{{AB}}\).
C. \(\tan B = \frac{{AC}}{{AB}}\).
D. \(\cot C = \frac{{AB}}{{BC}}\).
Phương pháp giải:
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có:
+ Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề gọi là tan của \(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối gọi là cot của \(\alpha \).
Lời giải chi tiết:
Vì tam giác ABC có \(\widehat A = {90^o}\) nên \(\tan B = \frac{{AC}}{{AB}}\)
Chọn C
Trả lời Câu 3 trang 72 Vở thực hành Toán 9
Cho \(\alpha \), \(\beta \) là hai góc nhọn trong tam giác ABC (H.4.4). Khi đó
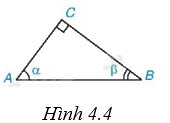
A. \(\sin \alpha = \tan \beta \).
B. \(\cos \alpha = \cot \beta \).
C. \(\tan \alpha = - \cot \beta \).
D. \(\cot \alpha = \tan \beta \).
Phương pháp giải:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Lời giải chi tiết:
Vì tam giác ABC vuông tại C nên \(\widehat A + \widehat B = {90^o}\), suy ra \(\alpha + \beta = {90^o}\). Do đó, \(\cot \alpha = \tan \beta \).
Chọn D
 Trả lời Câu 2 trang 72 Vở thực hành Toán 9
Trả lời Câu 2 trang 72 Vở thực hành Toán 9
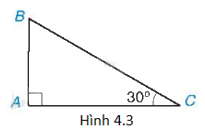
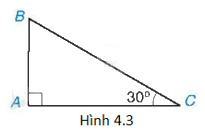
Cho tam giác ABC có \(\widehat A = {90^o}\) và \(\widehat C = {30^o}\) như trên Hình 4.3. Tìm khẳng định sai trong các khẳng định sau?
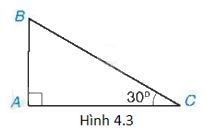
A. \(\sin B = \frac{{\sqrt 3 }}{2}\).
B. \(\cos C = \frac{{\sqrt 3 }}{2}\).
C. \(\tan B = \sqrt 3 \).
D. \(\cot B = \frac{1}{2}\).
Phương pháp giải:
+ Tính góc B.
+ Sử dụng bảng giá trị lượng giác của các góc 30 độ và 60 để tính.
Lời giải chi tiết:
Vì tam giác ABC có \(\widehat A = {90^o}\) nên \(\widehat B = {90^o} - \widehat C = {60^o}\).
Suy ra \(\sin B = \cos C = \sin {60^o} = \frac{{\sqrt 3 }}{2};\tan B = \tan {60^o} = \sqrt 3 ;\cot B = \cot {60^o} = \frac{{\sqrt 3 }}{3}\).
Chọn D
Chọn phương án đúng trong mỗi câu sau:
Trả lời Câu 1 trang 72 Vở thực hành Toán 9
Cho tam giác ABC có \(\widehat A = {90^o}\) (H 4.2).
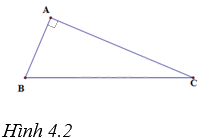
A. \(\sin B = \frac{{AB}}{{BC}}\).
B. \(\cos C = \frac{{AC}}{{AB}}\).
C. \(\tan B = \frac{{AC}}{{AB}}\).
D. \(\cot C = \frac{{AB}}{{BC}}\).
Phương pháp giải:
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có:
+ Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề gọi là tan của \(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối gọi là cot của \(\alpha \).
Lời giải chi tiết:
Vì tam giác ABC có \(\widehat A = {90^o}\) nên \(\tan B = \frac{{AC}}{{AB}}\)
Chọn C
 Trả lời Câu 2 trang 72 Vở thực hành Toán 9
Trả lời Câu 2 trang 72 Vở thực hành Toán 9
Cho tam giác ABC có \(\widehat A = {90^o}\) và \(\widehat C = {30^o}\) như trên Hình 4.3. Tìm khẳng định sai trong các khẳng định sau?
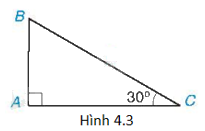
A. \(\sin B = \frac{{\sqrt 3 }}{2}\).
B. \(\cos C = \frac{{\sqrt 3 }}{2}\).
C. \(\tan B = \sqrt 3 \).
D. \(\cot B = \frac{1}{2}\).
Phương pháp giải:
+ Tính góc B.
+ Sử dụng bảng giá trị lượng giác của các góc 30 độ và 60 để tính.
Lời giải chi tiết:
Vì tam giác ABC có \(\widehat A = {90^o}\) nên \(\widehat B = {90^o} - \widehat C = {60^o}\).
Suy ra \(\sin B = \cos C = \sin {60^o} = \frac{{\sqrt 3 }}{2};\tan B = \tan {60^o} = \sqrt 3 ;\cot B = \cot {60^o} = \frac{{\sqrt 3 }}{3}\).
Chọn D
Trả lời Câu 3 trang 72 Vở thực hành Toán 9
Cho \(\alpha \), \(\beta \) là hai góc nhọn trong tam giác ABC (H.4.4). Khi đó
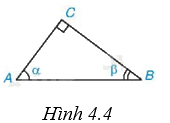
A. \(\sin \alpha = \tan \beta \).
B. \(\cos \alpha = \cot \beta \).
C. \(\tan \alpha = - \cot \beta \).
D. \(\cot \alpha = \tan \beta \).
Phương pháp giải:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Lời giải chi tiết:
Vì tam giác ABC vuông tại C nên \(\widehat A + \widehat B = {90^o}\), suy ra \(\alpha + \beta = {90^o}\). Do đó, \(\cot \alpha = \tan \beta \).
Chọn D
Trả lời Câu 4 trang 72 Vở thực hành Toán 9
A. \(\sin {82^o} = - \cos {8^o}\).
B. \(\cos {75^o} = \sin {16^o}\).
C. \(\cot {52^o} = - \tan {28^o}\).
D. \(\tan {30^o}40' = \cot {59^o}20'\).
Phương pháp giải:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Lời giải chi tiết:
Vì \({30^o}40' + {59^o}20' = {90^o}\) nên \(\tan {30^o}40' = \cot {59^o}20'\)
Chọn D
Trang 72 Vở thực hành Toán 9 thường chứa các bài tập trắc nghiệm liên quan đến một chủ đề cụ thể đã được học. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để đạt kết quả tốt trong các bài kiểm tra. Bài viết này sẽ cung cấp lời giải chi tiết cho từng câu hỏi trắc nghiệm, đồng thời phân tích các phương pháp giải hiệu quả.
Thông thường, trang 72 Vở thực hành Toán 9 tập trung vào các chủ đề như:
Dưới đây là giải chi tiết cho một số câu hỏi trắc nghiệm thường gặp trên trang 72 Vở thực hành Toán 9. (Lưu ý: Nội dung cụ thể sẽ thay đổi tùy theo phiên bản Vở thực hành)
Cho hệ phương trình: 2x + y = 5 x - y = 1
Hệ phương trình có nghiệm là:
Giải: Cộng hai phương trình, ta được: 3x = 6 => x = 2. Thay x = 2 vào phương trình x - y = 1, ta được: 2 - y = 1 => y = 1. Vậy nghiệm của hệ phương trình là (2, 1). Đáp án: A
Phương trình x2 - 4x + 3 = 0 có nghiệm là:
Giải: Tính delta: Δ = (-4)2 - 4 * 1 * 3 = 16 - 12 = 4. Vì Δ > 0, phương trình có hai nghiệm phân biệt: x1 = (4 + √4) / 2 = 3 và x2 = (4 - √4) / 2 = 1. Đáp án: A
Để giải các bài tập trắc nghiệm Toán 9 một cách hiệu quả, bạn nên:
Việc giải các câu hỏi trắc nghiệm trang 72 Vở thực hành Toán 9 không chỉ giúp bạn củng cố kiến thức mà còn chuẩn bị cho các kỳ thi quan trọng như kiểm tra giữa học kỳ, kiểm tra cuối học kỳ và kỳ thi tuyển sinh vào THPT. Ngoài ra, việc giải bài tập còn giúp bạn phát triển tư duy logic, khả năng phân tích và giải quyết vấn đề.
Toán 9 là một môn học quan trọng, đòi hỏi sự chăm chỉ và kiên trì. Hãy dành thời gian ôn tập lý thuyết, làm bài tập và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Đừng ngại đặt câu hỏi và thảo luận về các vấn đề chưa hiểu rõ. Chúc bạn học tốt môn Toán 9!
| Công thức | Mô tả |
|---|---|
| Δ = b2 - 4ac | Tính delta của phương trình bậc hai |
| x1,2 = (-b ± √Δ) / 2a | Tính nghiệm của phương trình bậc hai |