Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 90 Vở thực hành Toán 9 tập 2 trên giaitoan.edu.vn. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho tam giác nhọn ABC cân tại đỉnh A. Đường tròn đường kính BC cắt các cạnh AB, AC của tam giác ABC lần lượt tại F và E. a) Cho BE cắt CF tại H. Chứng minh rằng AH vuông góc với BC. b) Chứng minh rằng EF song song với BC.
Đề bài
Cho tam giác nhọn ABC cân tại đỉnh A. Đường tròn đường kính BC cắt các cạnh AB, AC của tam giác ABC lần lượt tại F và E.
a) Cho BE cắt CF tại H. Chứng minh rằng AH vuông góc với BC.
b) Chứng minh rằng EF song song với BC.
Phương pháp giải - Xem chi tiết
a) Chứng minh \(BE \bot AC,CF \bot AB\), suy ra H là trực tâm tam giác ABC nên AH vuông góc với BC.
b) Chứng minh \(\widehat {EFC} = \widehat {EBC}\), \(\widehat {EBC} = {90^o} - \widehat {ECB} = {90^o} - \widehat {FBC} = \widehat {FCB}\) nên \(\widehat {EFC} = \widehat {FCB}\), suy ra EF//BC.
Lời giải chi tiết
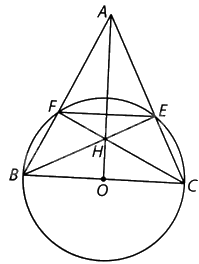
a) Gọi O là đường tròn đường kính BC. Vì \(\widehat {BEC}\) và \(\widehat {CFB}\) là các góc nội tiếp của (O) cùng chắn nửa đường tròn nên \(\widehat {BEC} = \widehat {CFB} = {90^o}\). Suy ra \(BE \bot AC,CF \bot AB\). Do đó H là trực tâm của tam giác ABC. Vì vậy AH vuông góc với BC.
b) Vì \(\widehat {EFC}\) và \(\widehat {EBC}\) là các góc nội tiếp của (O) cùng chắn nên \(\widehat {EFC} = \widehat {EBC}\) (1)
Mặt khác, tam giác ABC cân tại A và các tam giác BCF, CBE lần lượt vuông tại F và E nên \(\widehat {EBC} = {90^o} - \widehat {ECB} = {90^o} - \widehat {FBC} = \widehat {FCB}\). (2)
Từ (1) và (2) ta suy ra \(\widehat {EFC} = \widehat {FCB}\). Do đó EF//BC (hai góc ở vị trí so le trong)
Bài 8 trang 90 Vở thực hành Toán 9 tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về hàm số để giải quyết các bài toán thực tế, hoặc chứng minh các tính chất liên quan đến hàm số.
Bài 8 thường bao gồm các dạng bài tập sau:
Để giải bài 8 trang 90 Vở thực hành Toán 9 tập 2 hiệu quả, các em cần nắm vững các kiến thức sau:
Ví dụ: Cho hàm số y = 2x - 3. Hãy xác định xem hàm số này có phải là hàm số bậc nhất hay không? Nếu có, hãy xác định hệ số a và b.
Giải:
Hàm số y = 2x - 3 là hàm số bậc nhất vì nó có dạng y = ax + b, trong đó a = 2 và b = -3. Hệ số a = 2 và b = -3.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong Vở thực hành Toán 9 tập 2, hoặc tìm kiếm trên các trang web học Toán online uy tín.
Khi giải bài tập về hàm số, các em nên vẽ đồ thị của hàm số để hình dung rõ hơn về tính chất của nó. Điều này sẽ giúp các em dễ dàng giải quyết các bài toán phức tạp hơn.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Phương trình hàm số bậc nhất |
| a | Hệ số góc |
| b | Tung độ gốc |
Hy vọng với những kiến thức và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn khi giải bài 8 trang 90 Vở thực hành Toán 9 tập 2 và các bài tập tương tự. Chúc các em học tập tốt!