Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 3 trang 120, 121 Vở thực hành Toán 9 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho đường tròn (O) đường kính AB, tiếp tuyến xx’ tại A và tiếp tuyến yy’ tại B của (O). Một tiếp tuyến thứ ba của (O) tại điểm P (P khác A và B) cắt xx’ tại M và cắt yy’ tại N. a) Chứng minh rằng (MN = MA + NB). b) Đường thẳng đi qua O và vuông góc với AB cắt MN tại Q. Chứng minh rằng Q là trung điểm của đoạn MN. c) Chứng minh rằng AB tiếp xúc với đường tròn đường kính MN.
Đề bài
Cho đường tròn (O) đường kính AB, tiếp tuyến xx’ tại A và tiếp tuyến yy’ tại B của (O). Một tiếp tuyến thứ ba của (O) tại điểm P (P khác A và B) cắt xx’ tại M và cắt yy’ tại N.
a) Chứng minh rằng \(MN = MA + NB\).
b) Đường thẳng đi qua O và vuông góc với AB cắt MN tại Q. Chứng minh rằng Q là trung điểm của đoạn MN.
c) Chứng minh rằng AB tiếp xúc với đường tròn đường kính MN.
Phương pháp giải - Xem chi tiết
a) Chứng minh \(MA = MP\), \(NB = NP\) nên \(MA + NB = MP + PN = MN\).
b) + Chứng minh OQ//MA//NB. Nối A với N cắt OQ tại C.
+ Trong tam giác ABN, đường thẳng OQ đi qua trung điểm của cạnh AB và song song với BN nên C là trung điểm của AN
+ Trong tam giác AMN, đường thẳng OQ đi qua trung điểm của AN và song song với AM nên Q là trung điểm của MN.
c) + Chứng minh tam giác MON vuông tại O, suy ra \(OQ = QN = QM\)
+ Chứng minh đường tròn đường kính MN, cũng là đường tròn đi qua O. Do đó, AB vuông góc với OQ tại O. Suy ra AB là tiếp tuyến của đường tròn đường kính MN.
Lời giải chi tiết
(H.5.40)
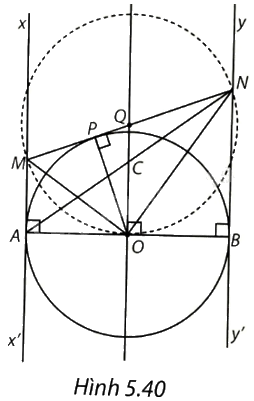
a) Ta có: $MN=MP+PN$. Mặt khác MA và MP là hai tiếp tuyến cắt nhau của (O) nên $MA=MP$.
Tương tự, ta cũng có $NB=NP$. Cộng từng vế hai đẳng thức trên ta được: $MA+NB=MP+PN=MN$ (điều phải chứng minh).
b) Do \(QO \bot AB\) (giả thiết), \(MA \bot AB\) và \(NB \bot AB\) (MA, NB là tiếp tuyến của (O) tại A và B) nên OQ//MA//NB. Nối A với N cắt OQ tại C.
Trong tam giác ABN, đường thẳng OQ đi qua trung điểm của cạnh AB và song song với BN nên C là trung điểm của AN.
Trong tam giác AMN, đường thẳng OQ đi qua trung điểm của AN và song song với AM nên Q là trung điểm của MN.
c) Theo tính chất của hai tiếp tuyến cắt nhau, OM là tia phân giác của góc AOP và ON là tia phân giác của góc POB. Khi đó:
\(\widehat {MON} = \widehat {MOP} + \widehat {NOP} \\= \frac{1}{2}\widehat {AOP} + \frac{1}{2}\widehat {BOP} \\= \frac{1}{2}\left( {\widehat {AOP} + \widehat {BOP}} \right) \\= \frac{1}{2}\widehat {AOB} = {90^o}\)
Do đó, tam giác MON là tam giác vuông tại O với OQ là đường trung tuyến. Từ đó ta có \(OQ = QN = QM\). Vậy đường tròn đường kính MN, cũng là đường tròn tâm Q đi qua O. Do đó, AB vuông góc với bán kính OQ tại O. Suy ra AB là tiếp tuyến của đường tròn đường kính MN.
Nói cách khác, AB tiếp xúc với đường tròn đường kính MN.
Bài 3 trang 120, 121 Vở thực hành Toán 9 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 3 bao gồm các dạng bài tập sau:
Để giải câu a, ta cần xác định hệ số góc và tung độ gốc của hàm số. Ví dụ, cho hàm số y = 2x + 3, hệ số góc là 2 và tung độ gốc là 3. Việc xác định chính xác hai yếu tố này là bước quan trọng để hiểu rõ tính chất của hàm số và vẽ đồ thị một cách chính xác.
Để vẽ đồ thị hàm số, ta cần xác định ít nhất hai điểm thuộc đồ thị. Ví dụ, với hàm số y = 2x + 3, ta có thể chọn x = 0, suy ra y = 3, và x = 1, suy ra y = 5. Vậy ta có hai điểm (0, 3) và (1, 5). Nối hai điểm này lại, ta được đồ thị hàm số.
Để tìm tọa độ giao điểm của hai đường thẳng, ta cần giải hệ phương trình tương ứng với hai đường thẳng đó. Ví dụ, cho hai đường thẳng y = x + 1 và y = -x + 3, ta giải hệ phương trình:
x + 1 = -x + 3
Suy ra 2x = 2, vậy x = 1. Thay x = 1 vào phương trình y = x + 1, ta được y = 2. Vậy tọa độ giao điểm của hai đường thẳng là (1, 2).
Khi giải bài tập về hàm số bậc nhất, bạn cần lưu ý những điều sau:
Xét hàm số y = -x + 2. Hệ số góc của hàm số là -1, tung độ gốc là 2. Đồ thị hàm số là một đường thẳng cắt trục Oy tại điểm (0, 2) và cắt trục Ox tại điểm (2, 0). Hàm số này nghịch biến trên R.
Bài 3 trang 120, 121 Vở thực hành Toán 9 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các lưu ý trên, bạn sẽ tự tin hơn trong quá trình giải bài tập và đạt kết quả tốt trong môn Toán 9.