Giải bài 11 trang 135, 136 Vở thực hành Toán 9 tập 2

Giải bài 11 trang 135, 136 vở thực hành Toán 9 tập 2

Giải bài 11 trang 135, 136 Vở thực hành Toán 9 tập 2

Chào mừng các em học sinh đến với lời giải chi tiết bài 11 trang 135, 136 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình đại số lớp 9, tập trung vào việc giải các bài toán liên quan đến hàm số bậc nhất.

Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết từng bước, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Tứ giác ABCD có hai góc đối diện B và D vuông, hai góc kia không vuông. a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Ta gọi đó là đường tròn (C). b) Gọi I và K lần lượt là trung điểm của các đường chéo AC và BD của tứ giác. Chứng minh rằng (IK bot BD). c) Kí hiệu các tiếp tuyến của đường tròn (C) tại A, B và C lần lượt là a, b và c. Giả sử b cắt a và c theo thứ tự tại E và F. Chứng minh rằng tứ giác AEFC là một hình thang. d) Chứng minh rằng (EF = AE + CF).

Đề bài

Tứ giác ABCD có hai góc đối diện B và D vuông, hai góc kia không vuông.

a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Ta gọi đó là đường tròn (C).

b) Gọi I và K lần lượt là trung điểm của các đường chéo AC và BD của tứ giác. Chứng minh rằng \(IK \bot BD\).

c) Kí hiệu các tiếp tuyến của đường tròn (C) tại A, B và C lần lượt là a, b và c. Giả sử b cắt a và c theo thứ tự tại E và F. Chứng minh rằng tứ giác AEFC là một hình thang.

d) Chứng minh rằng \(EF = AE + CF\).

Phương pháp giải - Xem chi tiết Giải bài 11 trang 135, 136 vở thực hành Toán 9 tập 2 1

a) Ta có \(\widehat {ABC} + \widehat {ADC} = {90^0} + {90^0} = {180^0}\) nên ABCD là tứ giác nội tiếp

b) + AC là đường kính của (C) nên I là tâm của (C).

+ Suy ra \(ID = IB\). Mà \(KD = KB\) nên IK là đường trung trực của DB. Vậy IK vuông góc với DB.

c) Vì \(AC \bot AE\), \(AC \bot CF\) suy ra AE // CF nên AEFC là hình thang.

d) Theo tính chất của tiếp tuyến có \(EB = EA,\;BF = FC\) nên \(EF = EB + BF = EA + FC\).

Lời giải chi tiết

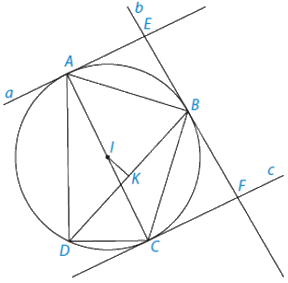
Giải bài 11 trang 135, 136 vở thực hành Toán 9 tập 2 2

a) Ta có \(\widehat {ABC} + \widehat {ADC} = {90^0} + {90^0} = {180^0}\) nên ABCD là tứ giác nội tiếp. Do vậy tồn tại đường tròn (C) đi qua bốn điểm A, B, C, D.

b) Ta có AC là đường kính của (C) (do AC chắn một cung \(90^\circ \)) nên I là tâm của (C). Từ đó \(ID = IB\), lại có \(KD = KB\) nên IK là đường trung trực của DB. Vậy IK vuông góc với DB.

c) Ta có \(AC \bot AE\), \(AC \bot CF\) suy ra AE // CF nên AEFC là hình thang.

d) Theo tính chất tiếp tuyến, ta có: \(EB = EA,\;BF = FC.\)

Do đó \(EF = EB + BF = EA + FC\).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 11 trang 135, 136 vở thực hành Toán 9 tập 2 đặc sắc thuộc chuyên mục giải bài tập toán lớp 9 trên nền tảng soạn toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 11 trang 135, 136 Vở thực hành Toán 9 tập 2: Hàm số bậc nhất

Bài 11 trang 135, 136 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Để giải bài tập này, các em cần nắm vững các khái niệm cơ bản như:

Hàm số bậc nhất: Hàm số có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0.
Đồ thị hàm số bậc nhất: Là một đường thẳng.
Hệ số góc a: Xác định độ dốc của đường thẳng.
Giao điểm với trục Oy: Điểm có tọa độ (0, b).

Nội dung bài tập:

Bài 11 thường bao gồm các dạng bài tập sau:

Xác định hàm số bậc nhất: Cho các thông tin về đường thẳng, yêu cầu xác định hàm số bậc nhất tương ứng.
Vẽ đồ thị hàm số bậc nhất: Cho hàm số, yêu cầu vẽ đồ thị của hàm số đó.
Tìm giao điểm của hai đường thẳng: Cho hai hàm số bậc nhất, yêu cầu tìm tọa độ giao điểm của hai đồ thị.
Ứng dụng hàm số bậc nhất vào giải quyết bài toán thực tế: Các bài toán liên quan đến vận tốc, quãng đường, thời gian,...

Hướng dẫn giải chi tiết:

Bài 11.1: Cho đường thẳng đi qua hai điểm A(1; 2) và B(3; 6). Hãy tìm hàm số bậc nhất có dạng y = ax + b biểu diễn đường thẳng này.

Giải:

Tìm hệ số góc a: a = (y₂ - y₁) / (x₂ - x₁) = (6 - 2) / (3 - 1) = 4 / 2 = 2
Tìm hệ số b: Thay tọa độ điểm A(1; 2) vào hàm số y = 2x + b, ta có: 2 = 2 * 1 + b => b = 0
Vậy hàm số cần tìm là: y = 2x

Bài 11.2: Vẽ đồ thị hàm số y = -x + 3.

Giải:

Xác định hai điểm thuộc đồ thị:

Khi x = 0, y = -0 + 3 = 3. Điểm A(0; 3)
Khi y = 0, 0 = -x + 3 => x = 3. Điểm B(3; 0)

Vẽ đồ thị: Nối hai điểm A và B bằng một đường thẳng, ta được đồ thị hàm số y = -x + 3.

Bài 11.3: Tìm tọa độ giao điểm của hai đường thẳng y = 2x - 1 và y = -x + 2.

Giải:

Để tìm giao điểm, ta giải hệ phương trình:

y = 2x - 1

y = -x + 2

Thay y = 2x - 1 vào phương trình thứ hai, ta có: 2x - 1 = -x + 2 => 3x = 3 => x = 1

Thay x = 1 vào phương trình y = 2x - 1, ta có: y = 2 * 1 - 1 = 1

Vậy tọa độ giao điểm của hai đường thẳng là (1; 1).

Lưu ý:

Khi giải bài tập về hàm số bậc nhất, các em cần chú ý đến các khái niệm cơ bản và các công thức liên quan.
Nên vẽ đồ thị hàm số để hiểu rõ hơn về tính chất của hàm số.
Rèn luyện kỹ năng giải bài tập thường xuyên để nắm vững kiến thức.

Tóm tắt kiến thức quan trọng:

Hàm số bậc nhất là một khái niệm quan trọng trong chương trình Toán 9. Việc nắm vững kiến thức về hàm số bậc nhất sẽ giúp các em giải quyết các bài toán liên quan một cách dễ dàng và hiệu quả. Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ học tốt môn Toán 9 và đạt kết quả cao trong các kỳ thi.