Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 1 trang 110 và 111 trong Vở thực hành Toán 9 tập 2, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp những giải pháp tối ưu, giúp bạn hiểu rõ bản chất của từng bài toán, không chỉ đơn thuần là đáp án.
Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rằng: a) Tứ giác AEHF nội tiếp đường tròn tâm I; b) ME, MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.
Đề bài
Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rằng:
a) Tứ giác AEHF nội tiếp đường tròn tâm I;
b) ME, MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.
Phương pháp giải - Xem chi tiết
a) Chứng minh \(IE = IF = IH = IA\), suy ra tứ giác AEHF nội tiếp đường tròn (I, IA).
b) + Chứng minh tứ giác BCEF nội tiếp đường tròn (M, MB). Nên \(\widehat {AEF} = {180^o} - \widehat {FEC} = \widehat {FBC} = \widehat {ABC}\).
+ Chứng minh \(\widehat {IFA} = \widehat {IAF} = \widehat {HAB} = {90^o} - \widehat {ABC}\), \(\widehat {MFC} = \widehat {FCM}\),
suy ra \(\widehat {MFI} = \widehat {MFC} + \widehat {CFI}\)
\(= \widehat {MFC} + \left( {{{90}^o} - \widehat {IFA}} \right) \\= \left( {{{90}^o} - \widehat {ABC}} \right) + \widehat {ABC} = {90^o}\)
+ Do đó, \(MF \bot IF\) nên MF tiếp xúc với (I, IA).
+ Chứng minh tương tự ta có: ME tiếp xúc với (I, IA).
Lời giải chi tiết
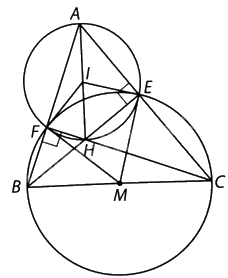
a) Do hai tam giác AEH và AFH vuông tại E và F nên \(IE = IF = IH = IA\). Vì vậy tứ giác AEHF nội tiếp đường tròn (I, IA).
b) Tương tự như trên, tứ giác BCEF có \(\widehat {BFC} = \widehat {BEC} = {90^o}\) nên tứ giác BCEF nội tiếp đường tròn (M, MB).
Suy ra \(\widehat {AEF} = {180^o} - \widehat {FEC} = \widehat {FBC} = \widehat {ABC}\).
Vì \(\Delta IFA\) cân tại I nên \(\widehat {IFA} = \widehat {IAF} = \widehat {HAB} = {90^o} - \widehat {ABC}\). (1)
Mặt khác, ta có \(MF = MC\), hay \(\Delta MFC\) cân tại M. Suy ra \(\widehat {MFC} = \widehat {FCM}\) (2)
Vì vậy ta có:
\(\widehat {MFI} = \widehat {MFC} + \widehat {CFI} \\= \widehat {MFC} + \left( {{{90}^o} - \widehat {IFA}} \right) \\= \left( {{{90}^o} - \widehat {ABC}} \right) + \widehat {ABC} \)
\(= {90^o}\) (theo (1) và (2)).
Do đó, \(MF \bot IF\). Suy ra MF tiếp xúc với (I, IA). Tương tự ME tiếp xúc với (I, IA).
Bài 1 trang 110, 111 Vở thực hành Toán 9 tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, liên quan đến việc xác định hàm số, vẽ đồ thị hàm số và ứng dụng hàm số vào việc giải quyết các vấn đề trong đời sống.
Bài 1 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh thực hiện các thao tác sau:
Để giải câu a, ta cần xác định hàm số bậc nhất có dạng y = ax + b. Dựa vào các thông tin đã cho, ta có thể lập hệ phương trình để tìm ra giá trị của a và b. Sau khi tìm được a và b, ta có thể viết được phương trình hàm số.
Ví dụ, nếu đề bài cho biết khi x = 1 thì y = 2 và khi x = 2 thì y = 4, ta có hệ phương trình:
Giải hệ phương trình này, ta được a = 2 và b = 0. Vậy hàm số cần tìm là y = 2x.
Để vẽ đồ thị hàm số, ta cần xác định một vài điểm thuộc đồ thị. Ta có thể chọn các giá trị của x và tính giá trị tương ứng của y. Sau đó, ta vẽ các điểm này lên mặt phẳng tọa độ và nối chúng lại để được đồ thị hàm số.
Ví dụ, với hàm số y = 2x, ta có thể chọn x = 0, x = 1, x = 2 và tính được y = 0, y = 2, y = 4. Vẽ các điểm (0, 0), (1, 2), (2, 4) lên mặt phẳng tọa độ và nối chúng lại, ta được đồ thị hàm số y = 2x.
Để ứng dụng hàm số vào việc giải quyết bài toán thực tế, ta cần hiểu rõ ý nghĩa của các đại lượng trong bài toán và cách chúng liên quan đến nhau. Sau đó, ta sử dụng hàm số để tính toán và tìm ra đáp án.
Ví dụ, nếu đề bài cho biết giá tiền của một sản phẩm là hàm số của số lượng sản phẩm mua, ta có thể sử dụng hàm số này để tính tổng số tiền phải trả khi mua một số lượng sản phẩm nhất định.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập tương tự trong Vở thực hành Toán 9 tập 2 và các tài liệu học tập khác.
Bài 1 trang 110, 111 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng, giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.