Bài 4 trang 112 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 112 VTH Toán 9 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
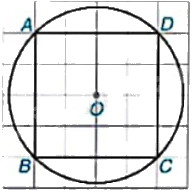
a) Cho hình vuông ABCD nội tiếp đường tròn (O) như hình bên. Phép quay thuận chiều ({45^o}) tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’ như hình bên. Hãy vẽ tứ giác A’B’C’D’. b) Phép quay trong câu a biến các điểm A’, B’, C’, D’ thành những điểm nào?
Đề bài
a) Cho hình vuông ABCD nội tiếp đường tròn (O) như hình bên. Phép quay thuận chiều \({45^o}\) tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’ như hình bên. Hãy vẽ tứ giác A’B’C’D’.
b) Phép quay trong câu a biến các điểm A’, B’, C’, D’ thành những điểm nào?
Phương pháp giải - Xem chi tiết
+ Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
+ Một phép quay được gọi là giữ nguyên một đa giác đều H nếu phép quay đó biến mỗi điểm của H thành một điểm của H.
Lời giải chi tiết
a) Ảnh của hình vuông ABCD qua phép quay thuận chiều 45o với tâm O là hình vuông A’B’C’D’ được vẽ như hình bên.
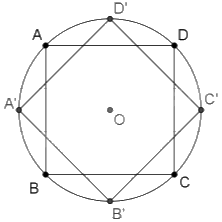
b) Phép quay trong câu a lại biến các điểm A’, B’, C’, D’ thành B, C, D, A.
Bài 4 trang 112 Vở thực hành Toán 9 tập 2 thuộc chương Hàm số bậc nhất. Bài tập này thường liên quan đến việc xác định hàm số, tìm giao điểm của đồ thị hàm số, hoặc giải các bài toán ứng dụng liên quan đến hàm số bậc nhất.
Bài 4 thường có dạng như sau: Cho hàm số y = ax + b. Tìm giá trị của a và b sao cho đồ thị hàm số đi qua hai điểm A(x1; y1) và B(x2; y2). Hoặc, bài tập có thể yêu cầu tìm điều kiện để hàm số đồng biến, nghịch biến.
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
(Ở đây sẽ là lời giải chi tiết của bài tập, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Ví dụ:)
Bài 4: Cho hàm số y = 2x + b. Tìm giá trị của b sao cho đồ thị hàm số đi qua điểm A(1; 3).
Giải:
Vì đồ thị hàm số đi qua điểm A(1; 3) nên ta thay x = 1 và y = 3 vào phương trình hàm số:
3 = 2 * 1 + b
=> b = 3 - 2
=> b = 1
Vậy, giá trị của b là 1.
Ngoài bài 4, Vở thực hành Toán 9 tập 2 còn nhiều bài tập tương tự. Học sinh có thể luyện tập thêm các bài tập sau để củng cố kiến thức:
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, học sinh nên:
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:
Bài 4 trang 112 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn khi làm bài tập Toán 9.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| a > 0 | Hàm số đồng biến |
| a < 0 | Hàm số nghịch biến |