Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 108 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết từng bước, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều kim đồng hồ. Phép quay thuận chiều ({45^o}) biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H. a) Vẽ đa giác EAFBGCHD. b) Đa giác EAFBGCHD có phải là một hình bát giác đều hay không? Vì sao?
Đề bài
Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều kim đồng hồ. Phép quay thuận chiều \({45^o}\) biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.
a) Vẽ đa giác EAFBGCHD.
b) Đa giác EAFBGCHD có phải là một hình bát giác đều hay không? Vì sao?
Phương pháp giải - Xem chi tiết
a) Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
b) + Chứng minh các tam giác AOE, BOF, COG, DOH, EOD, FOA, GOB, HOC bằng nhau theo trường hợp cạnh-góc-cạnh.
Suy ra EA = AF = FB = BG = GC = CH = HD = DE.
+ Bát giác \(EAFBGCHD\) lồi có các cạnh bằng nhau và nội tiếp đường tròn \((O).\)
Suy ra, các đỉnh của bát giác chia đường tròn thành 8 cung nhỏ với số đo mỗi cũng là 45o.
Từ đó, tính được các góc của bát giác bằng nhau và bằng 270 độ.
Do đó, \(EAFBGCHD\) là bát giác đều.
Lời giải chi tiết
a) Các điểm \(E,F,G,H\) cùng nằm trên đường tròn \(\left( O \right)\) và được vẽ như hình bên.
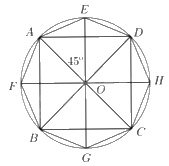
Do \(\widehat {AOE} = \widehat {BOF} = \widehat {COG} = \widehat {DOH} = {45^ \circ }\) nên \(\widehat {EOD} = \widehat {FOA} = \widehat {GOB} = \widehat {HOC} = {45^ \circ }\) (vì các tam giác\(AOD,BOA,COB,DOC\) vuông cân tại O).
Do vậy các tam giác AOE, BOF, COG, DOH, EOD, FOA, GOB, HOC bằng nhau theo trường hợp cạnh-góc-cạnh.
Suy ra EA = AF = FB = BG = GC = CH = HD = DE.
Vậy bát giác \(EAFBGCHD\) lồi có các cạnh bằng nhau và nội tiếp đường tròn \((O).\)
Hơn nữa các đỉnh của bát giác chia đường tròn thành 8 cung nhỏ với số đo mỗi cũng là 45o.
Do vậy các góc của bát giác lồi là các góc nội tiếp chắn đúng 6 cung nhỏ trên nên bằng nhau và có số đo bằng \(\frac{6}{8}{.360^ \circ } = {270^ \circ }\).
Vậy \(EAFBGCHD\) là bát giác đều.
Bài 4 trang 108 Vở thực hành Toán 9 tập 2 thường xoay quanh các chủ đề về hàm số bậc nhất, hàm số bậc hai, hoặc các ứng dụng của hàm số trong thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Để cung cấp lời giải chính xác, chúng ta cần biết nội dung cụ thể của bài toán. Tuy nhiên, dưới đây là một ví dụ về cách tiếp cận và giải quyết một bài toán tương tự:
Cho hàm số y = 2x + 3. Hãy tìm giá trị của y khi x = 1; x = -2; x = 0.
Vậy, khi x = 1 thì y = 5; khi x = -2 thì y = -1; khi x = 0 thì y = 3.
Ngoài việc tính giá trị của hàm số, bài 4 trang 108 Vở thực hành Toán 9 tập 2 còn có thể xuất hiện các dạng bài tập sau:
Để giải các bài tập về hàm số một cách hiệu quả, học sinh nên:
Để củng cố kiến thức và kỹ năng giải bài tập, các em có thể tham khảo các bài tập tương tự sau:
Bài 4 trang 108 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số. Bằng cách nắm vững các kiến thức cơ bản, luyện tập thường xuyên và áp dụng các mẹo giải bài tập hiệu quả, các em có thể tự tin giải quyết bài toán này và đạt kết quả tốt trong môn Toán.
Hy vọng rằng lời giải chi tiết và các hướng dẫn trên sẽ giúp các em học sinh hiểu rõ hơn về bài 4 trang 108 Vở thực hành Toán 9 tập 2. Chúc các em học tập tốt!