Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 9. Chúng tôi hiểu rằng việc giải các bài tập trắc nghiệm trong Vở thực hành Toán 9 tập 2 có thể gặp nhiều khó khăn.
Do đó, chúng tôi đã biên soạn bộ giải đáp đầy đủ, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài.
Gieo đồng thời hai con xúc xắc cân đối, đồng chất. Xác suất để “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10” là A. (frac{7}{{36}}). B. (frac{2}{9}). C. (frac{1}{6}). D. (frac{5}{{36}}).
Trả lời Câu 3 trang 82 Vở thực hành Toán 9
Một túi đựng 4 viên bi có cùng khối lượng và kích thước, được đánh số 1; 2; 3; 4. Lấy ngẫu nhiên hai viên bi từ trong túi. Xác suất để tích hai số ghi trên hai viên bi lớn hơn 3 là
A. \(\frac{5}{7}\).
B. \(\frac{2}{3}\).
C. \(\frac{3}{4}\).
D. \(\frac{5}{6}\).
Phương pháp giải:
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết:
Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là các số trên hai viên bi trong túi. Vì lấy đồng thời 2 viên bi nên \(a \ne b\).
Do đó, không gian mẫu là: \(\Omega = \left\{ {\left( {1,2} \right),\left( {1,3} \right),\left( {1,4} \right),\left( {2,3} \right),\left( {2,4} \right),\left( {3,4} \right)} \right\}\) nên số phần tử của không gian mẫu \(\Omega \) là 6.
Vì lấy ngẫu nhiên hai viên bi từ trong túi nên các kết quả có thể xảy ra ở trên là đồng khả năng.
Có 4 kết quả thuận lợi của biến cố “Tích hai số ghi trên hai viên bi lớn hơn 3” là: (1, 4), (2, 3), (2, 4), (3, 4). Do đó, \(P = \frac{4}{6} = \frac{2}{3}\).
Chọn B
Trả lời Câu 2 trang 81 Vở thực hành Toán 9
Có hai túi I và II. Túi I chứa 4 tấm thẻ, đánh số 1; 2; 3; 4. Túi II chứa 5 tấm thẻ, đánh số 1; 2; 3; 4; 5. Rút ngẫu nhiên một tấm thẻ từ mỗi túi I và II. Xác suất để cả hai tấm thẻ rút ra đều ghi số chẵn là
A. \(\frac{1}{5}\).
B. \(\frac{3}{{20}}\).
C. \(\frac{1}{4}\).
D. \(\frac{4}{{21}}\).
Phương pháp giải:
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết:
Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là các số trên các thẻ ở hai túi I và II.
Ta có bảng miêu tả không gian mẫu là:
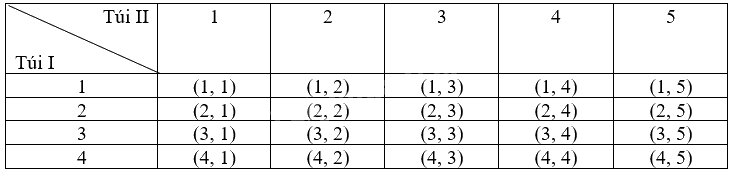
Do đó, số phần tử của không gian mẫu \(\Omega \) là 20.
Vì rút ngẫu nhiên một tấm thẻ từ mỗi túi I và II nên các kết quả có thể xảy ra ở trên là đồng khả năng.
Có 4 kết quả thuận lợi của biến cố “Hai tấm thẻ rút ra đều ghi số chẵn” là: (2, 2), (2, 4), (4, 2), (4, 4). Do đó, \(P = \frac{4}{{20}} = \frac{1}{5}\).
Chọn A
Trả lời Câu 1 trang 81 Vở thực hành Toán 9
Gieo đồng thời hai con xúc xắc cân đối, đồng chất. Xác suất để “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10” là
A. \(\frac{7}{{36}}\).
B. \(\frac{2}{9}\).
C. \(\frac{1}{6}\).
D. \(\frac{5}{{36}}\).
Phương pháp giải:
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết:
Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là số chấm xuất hiện trên hai con xúc xắc I và II.
Ta có bảng miêu tả không gian mẫu là:
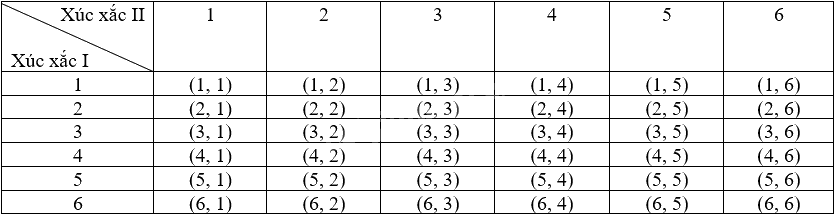
Do đó, số phần tử của không gian mẫu \(\Omega \) là 36.
Vì gieo đồng thời hai con xúc xắc cân đối, đồng chất nên các kết quả có thể xảy ra là đồng khả năng.
Có 6 kết quả thuận lợi của biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10” là: (4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6). Do đó, \(P = \frac{6}{{36}} = \frac{1}{6}\).
Chọn C
Chọn phương án trả lời đúng trong mỗi câu sau:
Trả lời Câu 1 trang 81 Vở thực hành Toán 9
Gieo đồng thời hai con xúc xắc cân đối, đồng chất. Xác suất để “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10” là
A. \(\frac{7}{{36}}\).
B. \(\frac{2}{9}\).
C. \(\frac{1}{6}\).
D. \(\frac{5}{{36}}\).
Phương pháp giải:
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết:
Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là số chấm xuất hiện trên hai con xúc xắc I và II.
Ta có bảng miêu tả không gian mẫu là:
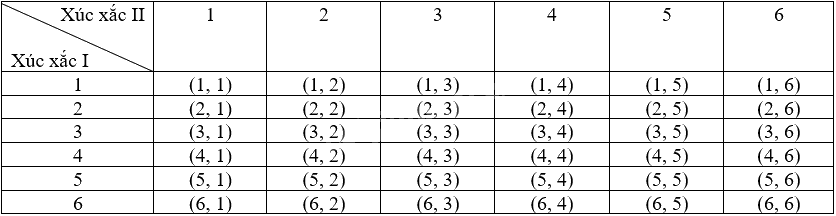
Do đó, số phần tử của không gian mẫu \(\Omega \) là 36.
Vì gieo đồng thời hai con xúc xắc cân đối, đồng chất nên các kết quả có thể xảy ra là đồng khả năng.
Có 6 kết quả thuận lợi của biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10” là: (4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6). Do đó, \(P = \frac{6}{{36}} = \frac{1}{6}\).
Chọn C
Trả lời Câu 2 trang 81 Vở thực hành Toán 9
Có hai túi I và II. Túi I chứa 4 tấm thẻ, đánh số 1; 2; 3; 4. Túi II chứa 5 tấm thẻ, đánh số 1; 2; 3; 4; 5. Rút ngẫu nhiên một tấm thẻ từ mỗi túi I và II. Xác suất để cả hai tấm thẻ rút ra đều ghi số chẵn là
A. \(\frac{1}{5}\).
B. \(\frac{3}{{20}}\).
C. \(\frac{1}{4}\).
D. \(\frac{4}{{21}}\).
Phương pháp giải:
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết:
Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là các số trên các thẻ ở hai túi I và II.
Ta có bảng miêu tả không gian mẫu là:
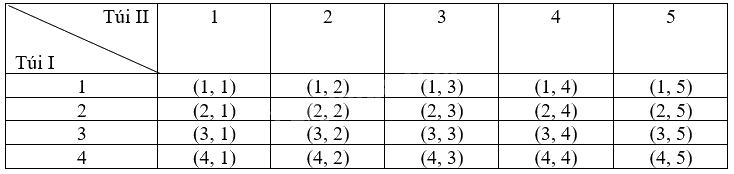
Do đó, số phần tử của không gian mẫu \(\Omega \) là 20.
Vì rút ngẫu nhiên một tấm thẻ từ mỗi túi I và II nên các kết quả có thể xảy ra ở trên là đồng khả năng.
Có 4 kết quả thuận lợi của biến cố “Hai tấm thẻ rút ra đều ghi số chẵn” là: (2, 2), (2, 4), (4, 2), (4, 4). Do đó, \(P = \frac{4}{{20}} = \frac{1}{5}\).
Chọn A
Trả lời Câu 3 trang 82 Vở thực hành Toán 9
Một túi đựng 4 viên bi có cùng khối lượng và kích thước, được đánh số 1; 2; 3; 4. Lấy ngẫu nhiên hai viên bi từ trong túi. Xác suất để tích hai số ghi trên hai viên bi lớn hơn 3 là
A. \(\frac{5}{7}\).
B. \(\frac{2}{3}\).
C. \(\frac{3}{4}\).
D. \(\frac{5}{6}\).
Phương pháp giải:
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết:
Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là các số trên hai viên bi trong túi. Vì lấy đồng thời 2 viên bi nên \(a \ne b\).
Do đó, không gian mẫu là: \(\Omega = \left\{ {\left( {1,2} \right),\left( {1,3} \right),\left( {1,4} \right),\left( {2,3} \right),\left( {2,4} \right),\left( {3,4} \right)} \right\}\) nên số phần tử của không gian mẫu \(\Omega \) là 6.
Vì lấy ngẫu nhiên hai viên bi từ trong túi nên các kết quả có thể xảy ra ở trên là đồng khả năng.
Có 4 kết quả thuận lợi của biến cố “Tích hai số ghi trên hai viên bi lớn hơn 3” là: (1, 4), (2, 3), (2, 4), (3, 4). Do đó, \(P = \frac{4}{6} = \frac{2}{3}\).
Chọn B
Trang 81 và 82 của Vở thực hành Toán 9 tập 2 thường tập trung vào các chủ đề như hàm số bậc nhất, hệ số góc, đường thẳng song song và vuông góc. Các câu hỏi trắc nghiệm ở đây đòi hỏi học sinh phải nắm vững định nghĩa, tính chất và các công thức liên quan. Việc giải đúng các bài tập này không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện kỹ năng giải quyết vấn đề.
Chúng ta sẽ đi vào giải chi tiết từng câu hỏi trắc nghiệm trên trang 81 và 82. Lưu ý rằng, trước khi xem lời giải, bạn nên tự mình thử sức giải bài để kiểm tra kiến thức và kỹ năng của mình.
Đề bài: ...
Lời giải: ...
Giải thích: ...
Đề bài: ...
Lời giải: ...
Giải thích: ...
Đề bài: ...
Lời giải: ...
Giải thích: ...
Để giải nhanh các bài tập trắc nghiệm, bạn có thể áp dụng một số mẹo sau:
Ví dụ: Cho đường thẳng y = 2x + 3. Xác định hệ số góc của đường thẳng này.
Lời giải: Hệ số góc của đường thẳng y = 2x + 3 là 2.
Để củng cố kiến thức và kỹ năng, bạn nên luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kinh nghiệm và học hỏi từ những người khác.
Việc giải các câu hỏi trắc nghiệm trang 81, 82 Vở thực hành Toán 9 tập 2 là một bước quan trọng trong quá trình học Toán 9. Hy vọng rằng, với bộ giải đáp chi tiết và các mẹo giải nhanh mà chúng tôi cung cấp, bạn sẽ tự tin hơn trong việc giải các bài tập và đạt kết quả tốt trong các kỳ thi.