Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 46, 47 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất và ứng dụng của nó trong giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Biểu đồ hình quạt tròn sau đây cho biết tỉ lệ lượt khách quốc tế đến Việt Nam trong năm 2022 bằng đường hàng không, đường bộ và đường biển. a) Lập bảng tần số tương đối cho dữ liệu được biểu diễn trên biểu đồ. b) Biết rằng năm 2022 có 3 277 000 lượt khách quốc tế đến Việt Nam bằng đường hàng không. Hãy tính số lượt khách quốc tế đến Việt Nam bằng đường bộ trong năm này.
Đề bài
Biểu đồ hình quạt tròn sau đây cho biết tỉ lệ lượt khách quốc tế đến Việt Nam trong năm 2022 bằng đường hàng không, đường bộ và đường biển.
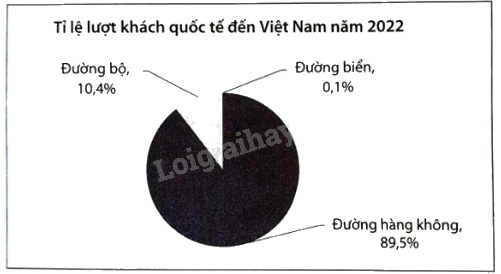
a) Lập bảng tần số tương đối cho dữ liệu được biểu diễn trên biểu đồ.
b) Biết rằng năm 2022 có 3 277 000 lượt khách quốc tế đến Việt Nam bằng đường hàng không. Hãy tính số lượt khách quốc tế đến Việt Nam bằng đường bộ trong năm này.
Phương pháp giải - Xem chi tiết
a) Lập bảng tần số tương đối:
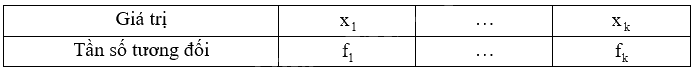
Trong đó, giá trị \({x_i}\) có tần số tương đối là \({f_i}\).
b) Số lượt khách quốc tế đến Việt Nam bằng đường bộ bằng 3 277 000. tần số tương đối khách quốc tế đến Việt Nam bằng đường hàng không.
Lời giải chi tiết
a) Ta có bảng tần số tương đối:

b) Số lượt khách đến Việt Nam bằng đường bộ năm 2022 là: 3 277 000.10,4%\( = 340\;808\) (khách)
Bài 4 trang 46, 47 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào việc giải quyết các bài toán liên quan đến đường thẳng và hệ số góc. Để giải bài tập này một cách hiệu quả, các em cần nắm vững các khái niệm cơ bản về hàm số bậc nhất, cách xác định hệ số góc và phương trình đường thẳng.
Bài 4 yêu cầu học sinh xác định hệ số góc của đường thẳng và viết phương trình đường thẳng khi biết các thông tin như tọa độ hai điểm thuộc đường thẳng, hệ số góc và một điểm thuộc đường thẳng, hoặc phương trình đường thẳng song song hoặc vuông góc với một đường thẳng cho trước.
Để giải bài 4 trang 46, 47 Vở thực hành Toán 9 tập 2, các em có thể áp dụng các phương pháp sau:
Câu a: (Ví dụ về một câu trong bài tập và lời giải chi tiết, bao gồm các bước thực hiện và giải thích rõ ràng). Ví dụ: Cho hai điểm A(1; 2) và B(3; 6). Hãy xác định hệ số góc của đường thẳng AB.
Lời giải: Hệ số góc của đường thẳng AB là m = (6 - 2) / (3 - 1) = 4 / 2 = 2.
Câu b: (Ví dụ về một câu trong bài tập và lời giải chi tiết). Ví dụ: Viết phương trình đường thẳng đi qua điểm C(0; -1) và có hệ số góc m = 3.
Lời giải: Phương trình đường thẳng có dạng y = 3x + b. Thay tọa độ điểm C(0; -1) vào phương trình, ta được -1 = 3 * 0 + b, suy ra b = -1. Vậy phương trình đường thẳng là y = 3x - 1.
Câu c: (Ví dụ về một câu trong bài tập và lời giải chi tiết). Ví dụ: Tìm phương trình đường thẳng song song với đường thẳng y = 2x + 1 và đi qua điểm D(2; 5).
Lời giải: Vì đường thẳng cần tìm song song với đường thẳng y = 2x + 1, nên hệ số góc của nó cũng là 2. Phương trình đường thẳng có dạng y = 2x + b. Thay tọa độ điểm D(2; 5) vào phương trình, ta được 5 = 2 * 2 + b, suy ra b = 1. Vậy phương trình đường thẳng là y = 2x + 1.
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, các em có thể tự giải các bài tập tương tự trong Vở thực hành Toán 9 tập 2 hoặc tham khảo các đề thi thử Toán 9. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
Khi giải bài tập về hàm số bậc nhất, các em cần lưu ý:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả này, các em sẽ học tập tốt môn Toán 9 và đạt kết quả cao trong các kỳ thi sắp tới.