Bạn đang gặp khó khăn trong việc giải các bài tập trắc nghiệm Toán 9 trang 77 và 78 trong Vở thực hành? giaitoan.edu.vn là địa chỉ tin cậy, cung cấp đáp án chi tiết và dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong các bài kiểm tra.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gây khó khăn, đặc biệt là với các dạng bài tập trắc nghiệm đòi hỏi sự nhanh nhạy và chính xác. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn bộ giải đáp này, với mục tiêu giúp bạn học Toán 9 một cách hiệu quả nhất.
Cho tam giác PQR như Hình 4.12. Khi đó ta có: A. (PQ = PR.sin P). B. (PQ = PR.cos R). C. (QR = PR.cos P). D. (QR = PR.cos R).
Trả lời Câu 1 trang 77 Vở thực hành Toán 9
Cho tam giác PQR như Hình 4.12. Khi đó ta có:
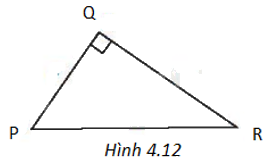
A. \(PQ = PR.\sin P\).
B. \(PQ = PR.\cos R\).
C. \(QR = PR.\cos P\).
D. \(QR = PR.\cos R\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải chi tiết:
Vì tam giác PQR vuông tại Q nên \(PQ = PR.\cos P = PR.\sin R\), \(QR = PR.\cos R\)
Chọn D
Trả lời Câu 4 trang 78 Vở thực hành Toán 9
Cho tam giác vuông MNP như Hình 4.14. Tìm khẳng định sai trong các khẳng định sau?
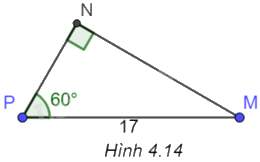
A. \(NP = 8,5\).
B. \(MN = \frac{{17\sqrt 3 }}{2}\).
C. \(NP = MN.\tan {60^o}\).
D. \(NP = MN.\cot {60^o}\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc nhân với côtang góc kề.
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải chi tiết:
Vì tam giác MNP vuông tại N nên:
+ \(NP = PM.\cos P = 17.\cos {60^o} = 8,5\)
+ \(MN = PM.\sin P = 17.\sin {60^o} = \frac{{17\sqrt 3 }}{2}\)
+ \(NP = MN.\tan M = MN.\tan \left( {{{90}^o} - {{60}^o}} \right) \) \(= MN.\tan {30^o};\)
\(NP = MN.\cot P = MN.\cot {60^o}\)
Chọn C
Trả lời Câu 1 trang 77 Vở thực hành Toán 9
Cho tam giác PQR như Hình 4.12. Khi đó
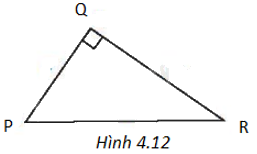
A. \(PQ = QR.\tan P\).
B. \(PQ = QR.\cot R\).
C. \(QR = PQ.\tan P\).
D. \(QR = PQ.\cot P\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc nhân với côtang góc kề.
Lời giải chi tiết:
Vì tam giác PQR vuông tại Q nên \(PQ = QR.\tan R = QR.\cot P\), \(QR = PQ.\tan P = PQ.\cot R\)
Chọn C
Trả lời Câu 3 trang 77 Vở thực hành Toán 9
Cho tam giác vuông MNP như Hình 4.13. Khi đó
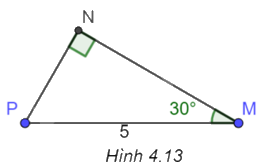
A. \(MN = \frac{5}{2}\).
B. \(MN = \frac{{5\sqrt 3 }}{3}\).
C. \(MN = 5\sqrt 3 \).
D. \(MN = \frac{{5\sqrt 3 }}{2}\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải chi tiết:
Vì tam giác MNP vuông tại N nên
\(MN = PM.\cos M = 5.\cos {30^o} = \frac{{5\sqrt 3 }}{2}\)
Chọn D
Chọn phương án đúng trong mỗi câu sau:
Trả lời Câu 1 trang 77 Vở thực hành Toán 9
Cho tam giác PQR như Hình 4.12. Khi đó ta có:
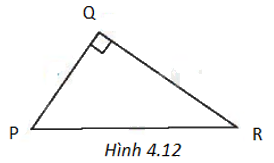
A. \(PQ = PR.\sin P\).
B. \(PQ = PR.\cos R\).
C. \(QR = PR.\cos P\).
D. \(QR = PR.\cos R\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải chi tiết:
Vì tam giác PQR vuông tại Q nên \(PQ = PR.\cos P = PR.\sin R\), \(QR = PR.\cos R\)
Chọn D
Trả lời Câu 1 trang 77 Vở thực hành Toán 9
Cho tam giác PQR như Hình 4.12. Khi đó
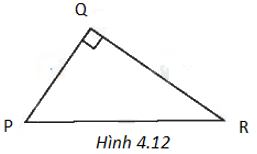
A. \(PQ = QR.\tan P\).
B. \(PQ = QR.\cot R\).
C. \(QR = PQ.\tan P\).
D. \(QR = PQ.\cot P\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc nhân với côtang góc kề.
Lời giải chi tiết:
Vì tam giác PQR vuông tại Q nên \(PQ = QR.\tan R = QR.\cot P\), \(QR = PQ.\tan P = PQ.\cot R\)
Chọn C
Trả lời Câu 3 trang 77 Vở thực hành Toán 9
Cho tam giác vuông MNP như Hình 4.13. Khi đó
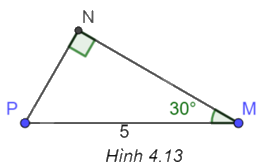
A. \(MN = \frac{5}{2}\).
B. \(MN = \frac{{5\sqrt 3 }}{3}\).
C. \(MN = 5\sqrt 3 \).
D. \(MN = \frac{{5\sqrt 3 }}{2}\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải chi tiết:
Vì tam giác MNP vuông tại N nên
\(MN = PM.\cos M = 5.\cos {30^o} = \frac{{5\sqrt 3 }}{2}\)
Chọn D
Trả lời Câu 4 trang 78 Vở thực hành Toán 9
Cho tam giác vuông MNP như Hình 4.14. Tìm khẳng định sai trong các khẳng định sau?
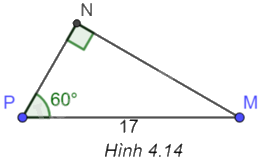
A. \(NP = 8,5\).
B. \(MN = \frac{{17\sqrt 3 }}{2}\).
C. \(NP = MN.\tan {60^o}\).
D. \(NP = MN.\cot {60^o}\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc nhân với côtang góc kề.
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải chi tiết:
Vì tam giác MNP vuông tại N nên:
+ \(NP = PM.\cos P = 17.\cos {60^o} = 8,5\)
+ \(MN = PM.\sin P = 17.\sin {60^o} = \frac{{17\sqrt 3 }}{2}\)
+ \(NP = MN.\tan M = MN.\tan \left( {{{90}^o} - {{60}^o}} \right) \) \(= MN.\tan {30^o};\)
\(NP = MN.\cot P = MN.\cot {60^o}\)
Chọn C
Trang 77 và 78 Vở thực hành Toán 9 tập trung vào các chủ đề quan trọng như hệ phương trình bậc hai hai ẩn, phương trình bậc hai một ẩn và ứng dụng thực tế. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là điều cần thiết để đạt kết quả tốt trong môn Toán.
Các câu hỏi trắc nghiệm trang 77 thường xoay quanh việc xác định điều kiện xác định của phương trình, tìm nghiệm của phương trình và kiểm tra xem một giá trị có phải là nghiệm của phương trình hay không. Để giải quyết những câu hỏi này, bạn cần nắm vững các khái niệm cơ bản về phương trình và bất phương trình.
Lưu ý: Khi giải các bài tập trắc nghiệm, hãy đọc kỹ đề bài, xác định rõ yêu cầu và loại trừ các đáp án sai trước khi chọn đáp án đúng.
Trang 78 Vở thực hành Toán 9 tiếp tục củng cố kiến thức về phương trình bậc hai một ẩn, đồng thời giới thiệu các phương pháp giải phương trình như phân tích thành nhân tử, sử dụng công thức nghiệm và phương pháp hoàn thiện bình phương.
Mẹo: Đối với các phương trình bậc hai, hãy luôn kiểm tra điều kiện xác định trước khi giải. Điều này sẽ giúp bạn tránh được những sai sót không đáng có.
Phương trình bậc hai không chỉ xuất hiện trong các bài tập Toán học mà còn có ứng dụng rộng rãi trong thực tế. Ví dụ, phương trình bậc hai có thể được sử dụng để tính toán quỹ đạo của một vật thể được ném lên không trung, hoặc để xác định kích thước tối ưu của một hình chữ nhật có diện tích cố định.
Một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Giả sử gia tốc trọng trường là 9.8 m/s2. Hãy tìm thời gian quả bóng đạt độ cao tối đa.
Giải:
Gọi t là thời gian quả bóng đạt độ cao tối đa. Khi đó, vận tốc của quả bóng tại thời điểm t là 0. Sử dụng công thức vận tốc: v = v0 - gt, ta có:
0 = 15 - 9.8t
t = 15 / 9.8 ≈ 1.53 giây
Kết luận:
Việc giải các câu hỏi trắc nghiệm trang 77, 78 Vở thực hành Toán 9 là một bước quan trọng trong quá trình học tập môn Toán 9. Hy vọng rằng với bộ giải đáp chi tiết và những lời khuyên hữu ích trên đây, bạn sẽ tự tin hơn trong việc chinh phục môn Toán và đạt được kết quả tốt nhất.