Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách Giải bài 4 trang 118 Vở thực hành Toán 9 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A. Một đường thẳng qua A cắt (O) tại B và cắt (O’) tại C. Chứng minh rằng OB//O’C.
Đề bài
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A. Một đường thẳng qua A cắt (O) tại B và cắt (O’) tại C. Chứng mỉnh rằng OB//O’C.
Phương pháp giải - Xem chi tiết
+ Chứng minh \(\widehat {OAB} = \widehat {O'AC}\), \(\widehat {OBA} = \widehat {OAB}\), \(\widehat {O'AC} = \widehat {O'CA}\) nên \(\widehat {OBA} = \widehat {O'CA}\).
+ Hai góc này ở vị trí so le trong nên OB//O’C.
Lời giải chi tiết
(H.5.37)
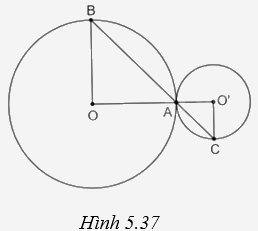
Do (O) và (O’) tiếp xúc ngoài với nhau tại A nên A thuộc OO’. Do đó, \(\widehat {OAB} = \widehat {O'AC}\) (hai góc đối đỉnh). Lại có \(\Delta OAB\) cân tại O \(\left( {OA = OB} \right)\) suy ra \(\widehat {OBA} = \widehat {OAB}\), \(\Delta O'AC\) cân tại O \(\left( {O'A = O'C} \right)\) suy ra \(\widehat {O'AC} = \widehat {O'CA}\). Từ đó suy ra \(\widehat {OBA} = \widehat {O'CA}\), mà hai góc này ở vị trí so le trong nên OB//O’C.
Bài 4 trang 118 Vở thực hành Toán 9 thuộc chương trình học về hàm số bậc nhất. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về xác định hàm số, tính giá trị của hàm số tại một điểm cho trước, và tìm điều kiện để hàm số đồng biến hoặc nghịch biến. Việc nắm vững các khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình Toán 9.
Bài 4 trang 118 Vở thực hành Toán 9 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 4 trang 118 Vở thực hành Toán 9, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. (Ở đây sẽ là lời giải chi tiết cho từng câu hỏi của bài 4, trang 118 VTH Toán 9. Ví dụ:)
Câu a) yêu cầu xác định hàm số y = 2x + 3 có phải là hàm số bậc nhất hay không. Để xác định, ta cần kiểm tra xem công thức có dạng y = ax + b hay không, trong đó a và b là các số thực. Trong trường hợp này, a = 2 và b = 3, do đó y = 2x + 3 là hàm số bậc nhất.
Câu b) yêu cầu tính giá trị của hàm số y = -x + 5 tại x = 2. Để tính, ta thay x = 2 vào công thức hàm số: y = -2 + 5 = 3. Vậy giá trị của hàm số tại x = 2 là 3.
Khi giải các bài tập về hàm số bậc nhất, các em cần lưu ý những điều sau:
Để củng cố kiến thức, các em có thể tham khảo các bài tập tương tự sau:
Hy vọng rằng với lời giải chi tiết và những lưu ý trên, các em học sinh đã có thể tự tin giải bài 4 trang 118 Vở thực hành Toán 9. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi!
| Dạng bài tập | Phương pháp giải |
|---|---|
| Xác định hàm số bậc nhất | Kiểm tra dạng y = ax + b |
| Tính giá trị hàm số | Thay x vào công thức |
| Tìm điều kiện đồng biến, nghịch biến | Xác định dấu của hệ số a |
| Nguồn: giaitoan.edu.vn | |