Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 123 Vở thực hành Toán 9 tập 2 trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng bắt đầu với bài giải chi tiết ngay sau đây!
Một bồn chứa xăng gồm hai nửa hình cầu có đường kính 1,8m và một hình trụ có chiều cao bằng 3,6m. Tính thể tích của bồn chứa xăng (làm tròn kết quả đến hàng phần trăm của ({m^3})).
Đề bài
Một bồn chứa xăng gồm hai nửa hình cầu có đường kính 1,8m và một hình trụ có chiều cao bằng 3,6m. Tính thể tích của bồn chứa xăng (làm tròn kết quả đến hàng phần trăm của \({m^3}\)).
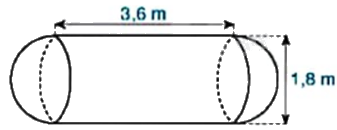
Phương pháp giải - Xem chi tiết
+ Tính thể tích hình trụ chiều cao 3,6m và bán kính \(\frac{{1,8}}{2}\)m.
+ Tính thể tích hai nửa hình cầu bán kính \(\frac{{1,8}}{2}\)m.
+ Thể tích bồn chứa xăng bằng tổng thể tích của hình trụ và hai nửa hình cầu trên.
Lời giải chi tiết
Thể tích bồn chứa xăng là:
\(\pi \cdot {\left( {\frac{{1,8}}{2}} \right)^2} \cdot 3,6 + \frac{4}{3}\pi \cdot {\left( {\frac{{1,8}}{2}} \right)^3} = \frac{{486\pi }}{{125}} \approx 12,21\,\,\left( {{{\rm{m}}^3}} \right)\).
Bài 5 trang 123 Vở thực hành Toán 9 tập 2 thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh xác định hệ số góc, điểm thuộc đồ thị hàm số, và giải các phương trình, bất phương trình liên quan.
Bài 5 thường bao gồm các dạng bài tập sau:
Để xác định hàm số bậc nhất y = ax + b, ta cần tìm hai điểm thuộc đồ thị hàm số. Sau đó, thay tọa độ hai điểm này vào phương trình hàm số để giải hệ phương trình tìm a và b.
Ví dụ:
Cho hàm số y = ax + b đi qua hai điểm A(1; 2) và B(-1; 0). Tìm a và b.
Giải:
Thay tọa độ điểm A vào phương trình hàm số, ta được: 2 = a(1) + b => a + b = 2 (1)
Thay tọa độ điểm B vào phương trình hàm số, ta được: 0 = a(-1) + b => -a + b = 0 (2)
Cộng (1) và (2), ta được: 2b = 2 => b = 1
Thay b = 1 vào (1), ta được: a + 1 = 2 => a = 1
Vậy hàm số cần tìm là y = x + 1.
Để kiểm tra xem một điểm M(x0; y0) có thuộc đồ thị hàm số y = ax + b hay không, ta thay x0 vào phương trình hàm số và tính y. Nếu y bằng y0 thì điểm M thuộc đồ thị hàm số, ngược lại thì không.
Ví dụ:
Cho hàm số y = 2x - 1. Điểm A(2; 3) có thuộc đồ thị hàm số hay không?
Giải:
Thay x = 2 vào phương trình hàm số, ta được: y = 2(2) - 1 = 3
Vì y = 3 bằng tung độ của điểm A, nên điểm A thuộc đồ thị hàm số.
Khi giải phương trình, bất phương trình liên quan đến hàm số, ta thường sử dụng các phương pháp đại số như giải phương trình bậc nhất một ẩn, giải bất phương trình bậc nhất một ẩn, hoặc sử dụng đồ thị hàm số để tìm nghiệm.
Trong các bài toán thực tế, việc xây dựng hàm số là bước quan trọng nhất. Ta cần xác định rõ các đại lượng liên quan, mối quan hệ giữa chúng, và chọn hệ tọa độ phù hợp để biểu diễn hàm số.
Hy vọng với hướng dẫn chi tiết này, các em học sinh đã có thể tự tin giải bài 5 trang 123 Vở thực hành Toán 9 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!