Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 74 Vở thực hành Toán 9. Bài học này thuộc chương trình Toán 9, tập trung vào việc vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp đáp án và lời giải bài tập Toán 9 một cách chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và (sqrt 3 ). Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác của các góc đặc biệt).
Đề bài
Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và \(\sqrt 3 \). Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác của các góc đặc biệt).
Phương pháp giải - Xem chi tiết
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có tỉ số giữa cạnh đối và cạnh kề gọi là tan của \(\alpha \).
Lời giải chi tiết
(H.4.8)
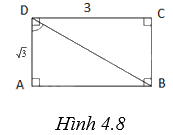
Hình chữ nhật ABCD có \(AD = \sqrt 3 ,DC = 3\). Ta cần tính góc ADB.
Ta có \(\tan \widehat {ADB} = \frac{{AB}}{{AD}} = \frac{3}{{\sqrt 3 }} = \sqrt 3 \)
Theo bảng giá trị lượng giác của các góc đặc biệt, ta có \(\widehat {ADB} = {60^o}\).
Bài 4 trang 74 Vở thực hành Toán 9 thường xoay quanh các chủ đề về hàm số bậc nhất, hệ số góc, và ứng dụng của hàm số trong việc giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số, đặc biệt là cách xác định hệ số góc và phương trình đường thẳng.
Trước khi bắt tay vào giải bài toán, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, cần phân tích mối quan hệ giữa các yếu tố này và tìm ra phương pháp giải phù hợp.
Thông thường, bài toán sẽ yêu cầu học sinh xác định hệ số góc của đường thẳng, viết phương trình đường thẳng, hoặc giải các bài toán liên quan đến ứng dụng của hàm số.
Để cung cấp lời giải chi tiết, cần biết chính xác nội dung của bài 4 trang 74 Vở thực hành Toán 9. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, có thể đưa ra một số hướng giải như sau:
Giả sử bài toán yêu cầu tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 6).
Giải:
Sau khi nắm vững phương pháp giải bài 4 trang 74 Vở thực hành Toán 9, học sinh nên luyện tập thêm với các bài tập tương tự để củng cố kiến thức và rèn luyện kỹ năng. Có thể tìm các bài tập trong sách giáo khoa, sách bài tập, hoặc trên các trang web học toán online.
Hy vọng với những hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài 4 trang 74 Vở thực hành Toán 9 và đạt kết quả tốt trong môn học Toán.
| Dạng bài tập | Phương pháp giải |
|---|---|
| Xác định hệ số góc | Sử dụng công thức a = (y2 - y1) / (x2 - x1) |
| Viết phương trình đường thẳng | Sử dụng phương trình y = ax + b |
| Ứng dụng hàm số vào giải bài toán thực tế | Phân tích bài toán, lập phương trình, giải phương trình |