Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 7 Vở thực hành Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng hành cùng các em trên con đường chinh phục môn Toán.
Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau: a) (2x - y = 3); b) (0x + 2y = - 4); c) (3x + 0y = 5).
Đề bài
Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:
a) \(2x - y = 3\);
b) \(0x + 2y = - 4\);
c) \(3x + 0y = 5\).
Phương pháp giải - Xem chi tiết
+ Từ phương trình đầu bài cho, ta tính x theo y hoặc y theo x, từ đó kết luận được nghiệm tổng quát của phương trình.
+ Biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn là đường thẳng \(ax + by = c\).
Lời giải chi tiết
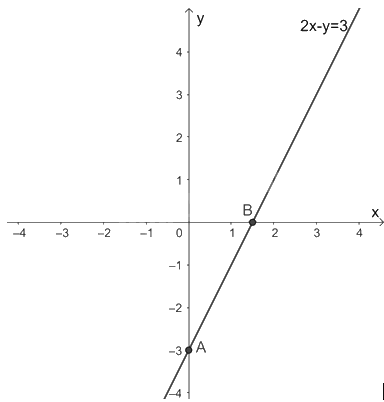
a) Xét phương trình \(2x - y = 3\). (1)
Ta viết (1) dưới dạng \(y = 2x - 3\). Khi đó, phương trình (1) có nghiệm là \(\left( {x;2x - 3} \right)\) với \(x \in \mathbb{R}\) tùy ý. Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng d: \(2x - y = 3\).
Ta có: \(A\left( {0; - 3} \right)\) và \(B\left( {\frac{3}{2};0} \right)\) là hai điểm nằm trên đường thẳng d nên ta có hình vẽ biểu diễn tập nghiệm của phương trình (1) như sau:
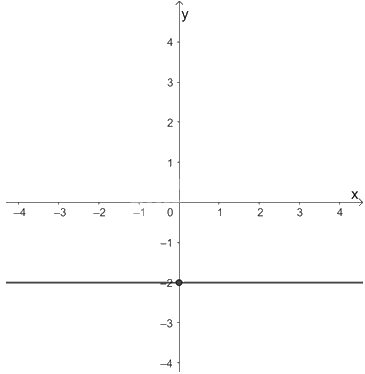
b) Xét phương trình \(0x + 2y = - 4\). (2)
Ta viết gọn (2) thành \(y = - 2\). Phương trình (2) có nghiệm là \(\left( {x; - 2} \right)\) với \(x \in \mathbb{R}\) tùy ý. Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục hoành cắt trục tung tại điểm \(\left( {0; - 2} \right)\). Ta gọi đó là đường thẳng \(y = - 2\) nên ta có hình vẽ biểu diễn tập nghiệm của phương trình (2) như sau:
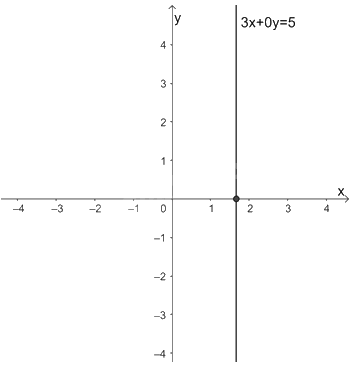
c) Xét phương trình \(3x + 0y = 5\). (3)
Ta viết gọn (3) thành \(x = \frac{5}{3}\). Phương trình (3) có nghiệm là \(\left( {\frac{5}{3};y} \right)\) với \(y \in \mathbb{R}\) tùy ý. Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục tung và cắt trục tung tại điểm \(\left( {\frac{5}{3};0} \right)\). Ta gọi đó là đường thẳng \(x = \frac{5}{3}\) nên ta có hình vẽ biểu diễn tập nghiệm của phương trình (3) như sau:
Bài 3 trang 7 Vở thực hành Toán 9 thường thuộc các chủ đề cơ bản như đại số, hình học, hoặc các bài toán thực tế ứng dụng. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững kiến thức nền tảng, hiểu rõ yêu cầu của đề bài và áp dụng các phương pháp giải phù hợp.
Bước đầu tiên trong quá trình giải bài tập Toán là đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu cần tìm. Điều này giúp học sinh tránh được những sai sót không đáng có và tập trung vào việc giải quyết vấn đề một cách chính xác.
Sau khi đã hiểu rõ đề bài, học sinh cần nhớ lại các kiến thức, định lý, công thức liên quan đến chủ đề của bài tập. Việc áp dụng đúng kiến thức là yếu tố then chốt để giải quyết bài toán một cách thành công.
Trước khi bắt tay vào giải bài tập, học sinh nên lập một kế hoạch giải cụ thể, bao gồm các bước thực hiện và các phép tính cần thiết. Việc này giúp học sinh có một cái nhìn tổng quan về bài toán và tránh được những sai sót trong quá trình tính toán.
(Nội dung lời giải chi tiết bài 3 trang 7 Vở thực hành Toán 9 sẽ được trình bày tại đây. Bao gồm các bước giải, giải thích rõ ràng và các lưu ý quan trọng. Ví dụ:)
Ví dụ: Bài 3: Cho biểu thức A = (x + 2)(x - 2) + 5. Hãy tìm giá trị của x để A = 9.
Ngoài bài 3 trang 7, Vở thực hành Toán 9 còn có nhiều bài tập tương tự khác. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để học Toán 9 hiệu quả, học sinh cần:
Bài 3 trang 7 Vở thực hành Toán 9 là một bài tập cơ bản, nhưng lại đóng vai trò quan trọng trong việc giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải Toán. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn trong quá trình học tập và đạt được kết quả tốt nhất.