Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 32 Vở thực hành Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, hỗ trợ các em học Toán 9 một cách toàn diện.
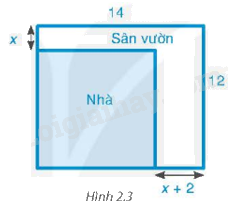
Bác An có một mảnh đất hình chữ nhật có chiều dài 14m và chiều rộng 12m. Bác dự định xây nhà trên mảnh đất đó và dành một diện tích đất để làm sân vườn như hình bên. Biết diện tích đất làm nhà là (100{m^2}). Hỏi x bằng bao nhiêu mét?
Đề bài
Bác An có một mảnh đất hình chữ nhật có chiều dài 14m và chiều rộng 12m. Bác dự định xây nhà trên mảnh đất đó và dành một diện tích đất để làm sân vườn như hình bên. Biết diện tích đất làm nhà là \(100{m^2}\). Hỏi x bằng bao nhiêu mét?
Phương pháp giải - Xem chi tiết
+ Dựa vào dữ kiện đầu bài, lập được phương trình có dạng phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\).
+ Để giải phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\), ta giải hai phương trình \(ax + b = 0\) và \(cx + d = 0\). Sau đó lấy tất cả các nghiệm của chúng.
Lời giải chi tiết
Phần đất làm nhà là một mảnh đất hình chữ nhật có chiều dài và chiều rộng lần lượt là \(14 - x - 2 = 12 - x\left( m \right)\) và \(12 - x\left( m \right)\). Diện tích đất làm nhà là \(\left( {12 - x} \right)\left( {12 - x} \right) = {\left( {12 - x} \right)^2}\;\left( {{m^2}} \right)\)
Ta có: \({\left( {12 - x} \right)^2} = 100\)
\({\left( {12 - x} \right)^2} = {10^2}\)
\({\left( {12 - x} \right)^2} - {10^2} = 0\)
\(\left( {12 - x - 10} \right)\left( {12 - x + 10} \right) = 0\)
\(\left( {2 - x} \right)\left( {22 - x} \right) = 0\)
Giải phương trình trên, kết hợp với điều kiện của x, ta được \(x = 2\).
Bài 4 trang 32 Vở thực hành Toán 9 thường thuộc các chủ đề về hàm số bậc nhất, hệ số góc, đường thẳng song song và vuông góc. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các công thức liên quan.
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực. Hệ số a được gọi là hệ số góc của đường thẳng biểu diễn hàm số. Hệ số góc a quyết định độ dốc của đường thẳng:
Cho hai đường thẳng có phương trình:
Khi đó:
Để giải bài 4 trang 32 Vở thực hành Toán 9, chúng ta cần phân tích đề bài và xác định yêu cầu. Thông thường, bài tập sẽ yêu cầu:
Giả sử đề bài yêu cầu tìm phương trình đường thẳng đi qua điểm A(1; 2) và song song với đường thẳng y = 3x - 1.
Lời giải:
Vì đường thẳng cần tìm song song với đường thẳng y = 3x - 1 nên nó có cùng hệ số góc, tức là a = 3. Vậy phương trình đường thẳng cần tìm có dạng y = 3x + b.
Thay tọa độ điểm A(1; 2) vào phương trình, ta được: 2 = 3 * 1 + b => b = -1.
Vậy phương trình đường thẳng cần tìm là y = 3x - 1.
Ngoài dạng bài tập tìm phương trình đường thẳng, bài 4 trang 32 Vở thực hành Toán 9 còn có thể xuất hiện các dạng bài tập khác như:
Để giải các dạng bài tập này, học sinh cần vận dụng linh hoạt các kiến thức đã học và kết hợp với các kỹ năng giải toán cơ bản.
Để nắm vững kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, học sinh nên luyện tập thường xuyên với các bài tập tương tự. Các em có thể tìm thấy nhiều bài tập luyện tập trong sách giáo khoa, sách bài tập và trên các trang web học Toán online.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Phương trình hàm số bậc nhất |
| a1 = a2 | Điều kiện hai đường thẳng song song |
| a1 * a2 = -1 | Điều kiện hai đường thẳng vuông góc |
Hy vọng với những kiến thức và phương pháp giải bài tập được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi giải bài 4 trang 32 Vở thực hành Toán 9 và các bài tập tương tự. Chúc các em học tập tốt!