Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 9 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình đại số lớp 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết từng bước, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một cổng vòm được thiết kế dạng parabol (y = a{x^2}) như hình dưới đây. Biết chiều rộng của chân cổng là (AB = 6m) và chiều cao cổng là (OI = 4,5m). a) Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa cổng I là 2m. b) Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2m, chiều cao 3m. Hỏi xe tải này có thể đi qua được cổng vòm đó hay không?
Đề bài
Một cổng vòm được thiết kế dạng parabol \(y = a{x^2}\) như hình dưới đây. Biết chiều rộng của chân cổng là \(AB = 6m\) và chiều cao cổng là \(OI = 4,5m\).
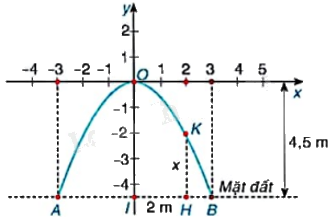
a) Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa cổng I là 2m.
b) Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2m, chiều cao 3m. Hỏi xe tải này có thể đi qua được cổng vòm đó hay không?
Phương pháp giải - Xem chi tiết
a) + Đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(\left( {3;4,5} \right)\). Thay tọa độ điểm \(\left( {3;4,5} \right)\) vào hàm số \(y = a{x^2}\) ta tìm được a.
+ \(HK = \left| { - 4,5 - \left( { - \frac{1}{2}{{.2}^2}} \right)} \right|\)
b) So sánh chiều cao và chiều rộng của xe tải và với chiều cao và chiều rộng của cổng vòm. Từ đó rút ra kết luận.
Lời giải chi tiết
a) Vì điểm \(\left( {3;4,5} \right)\) thuộc parabol nên ta có: \( - 4,5 = a{.3^2}\), suy ra \(a = - \frac{1}{2}\).
Từ đó ta có \(HK = \left| { - 4,5 - \left( { - \frac{1}{2}{{.2}^2}} \right)} \right| = 2,5\left( m \right)\).
b) Do xe tải có chiều rộng 2m nên ta tính chiều cao cổng tại vị trí cách I là 1m, tương ứng với \(x = 1\).
Tại \(x = 1\), chiều cao cổng là \(HK = \left| { - 4,5 - \left( { - \frac{1}{2}{{.1}^2}} \right)} \right| = 4\left( m \right)\).
Do chiều cao của cổng tại vị trí này lớn hơn chiều cao của xe tải nên xe tải này có thể đi qua được cổng vòm.
Bài 8 trang 9 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình ôn tập chương I về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và phân tích bài toán này:
Bài 8 yêu cầu học sinh thực hiện các nhiệm vụ sau:
a) Vẽ đồ thị của hàm số y = 2x + 1
Để vẽ đồ thị của hàm số y = 2x + 1, ta cần xác định hai điểm thuộc đồ thị. Chọn x = 0, ta có y = 2(0) + 1 = 1. Vậy điểm A(0; 1) thuộc đồ thị. Chọn x = 1, ta có y = 2(1) + 1 = 3. Vậy điểm B(1; 3) thuộc đồ thị.
Vẽ hệ trục tọa độ Oxy, đánh dấu hai điểm A(0; 1) và B(1; 3). Nối hai điểm này lại, ta được đồ thị của hàm số y = 2x + 1.
b) Xác định các điểm thuộc đồ thị hàm số
Để xác định một điểm thuộc đồ thị hàm số, ta chỉ cần thay giá trị của x vào phương trình hàm số và tính giá trị tương ứng của y. Ví dụ, nếu x = -1, thì y = 2(-1) + 1 = -1. Vậy điểm C(-1; -1) thuộc đồ thị hàm số.
c) Tìm giao điểm của đồ thị hàm số với trục hoành và trục tung
Giao điểm của đồ thị hàm số với trục tung là điểm có hoành độ x = 0. Thay x = 0 vào phương trình hàm số, ta được y = 2(0) + 1 = 1. Vậy giao điểm của đồ thị hàm số với trục tung là điểm A(0; 1).
Giao điểm của đồ thị hàm số với trục hoành là điểm có tung độ y = 0. Thay y = 0 vào phương trình hàm số, ta được 0 = 2x + 1. Giải phương trình này, ta được x = -1/2. Vậy giao điểm của đồ thị hàm số với trục hoành là điểm D(-1/2; 0).
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức về hàm số bậc nhất, các em có thể làm thêm các bài tập sau:
Bài 8 trang 9 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Hy vọng với lời giải chi tiết và phân tích trên, các em sẽ tự tin giải quyết bài tập này và các bài tập tương tự.
Lưu ý: Các em nên tự mình thực hiện các bước giải bài tập để hiểu rõ hơn về kiến thức và rèn luyện kỹ năng giải toán.