Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 9. Trang này tập trung vào việc giải các câu hỏi trắc nghiệm trang 74 Vở thực hành Toán 9 tập 2, giúp bạn củng cố kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải các bài tập trắc nghiệm đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, dễ hiểu, kèm theo các giải thích rõ ràng để bạn nắm vững phương pháp giải.
Bạn Sơn gieo một đồng xu cân đối và bạn Minh gieo đồng thời hai đồng xu cân đối. Xác suất để trong ba đồng xu có đúng một đồng xu xuất hiện mặt ngửa là A. (frac{2}{7}). B. (frac{1}{3}). C. (frac{3}{8}). D. (frac{1}{4}).
Trả lời Câu 2 trang 74 Vở thực hành Toán 9
Gieo con xúc xắc cân đối liên tiếp hai lần. Xác suất để trong hai lần gieo số chấm xuất hiện trên con xúc xắc đều là số nguyên tố là
A. \(\frac{7}{{36}}\).
B. \(\frac{8}{{35}}\).
C. \(\frac{3}{8}\).
D. \(\frac{2}{9}\).
Phương pháp giải:
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết:
Kết quả của phép thử là cặp số (a, b) trong đó a và b tương ứng là số chấm trên con xúc xắc 1 và xúc xắc 2.
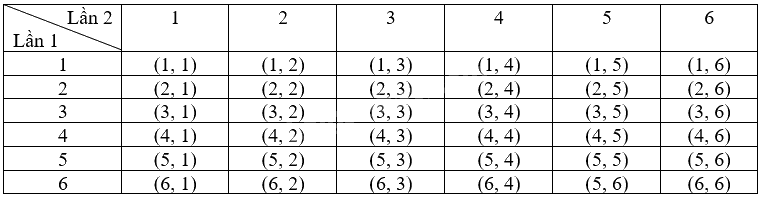Do đó, không gian mẫu có 36 phần tử, 36 kết quả có thể này là đồng khả năng
Có 9 kết quả thuận lợi của biến cố “Số chấm xuất hiện trên con xúc xắc trong hai lần gieo đều là số nguyên tố” là: (2, 2), (3, 2), (5, 2), (2, 3), (3, 3), (5, 3), (2, 5), (3, 5), (5, 5).
Xác suất của biến cố “Số chấm xuất hiện trên con xúc xắc trong hai lần gieo đều là số nguyên tố” là: \(\frac{9}{{36}} = \frac{1}{4}\).
Không có đáp án đúng
Trả lời Câu 1 trang 74 Vở thực hành Toán 9
Bạn Sơn gieo một đồng xu cân đối và bạn Minh gieo đồng thời hai đồng xu cân đối. Xác suất để trong ba đồng xu có đúng một đồng xu xuất hiện mặt ngửa là
A. \(\frac{2}{7}\).
B. \(\frac{1}{3}\).
C. \(\frac{3}{8}\).
D. \(\frac{1}{4}\).
Phương pháp giải:
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết:
Các kết quả có thể của hành động gieo đồng xu của Sơn là S, N và của Minh là (S, S); (N, S); (S, N); (N, N).
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng sau:
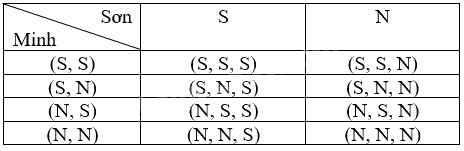
Số phần tử của không gian mẫu là 8. 8 kết quả này là đồng khả năng.
Có 3 kết quả thuận lợi của biến cố “Có đúng một đồng xu xuất hiện mặt ngửa” là: (S, S, N), (S, N, S), (N, S, S).
Vậy xác suất của biến cố “Có đúng một đồng xu xuất hiện mặt ngửa” là: \(\frac{3}{8}\).
Chọn C
Chọn phương án trả lời đúng trong mỗi câu sau:
Trả lời Câu 1 trang 74 Vở thực hành Toán 9
Bạn Sơn gieo một đồng xu cân đối và bạn Minh gieo đồng thời hai đồng xu cân đối. Xác suất để trong ba đồng xu có đúng một đồng xu xuất hiện mặt ngửa là
A. \(\frac{2}{7}\).
B. \(\frac{1}{3}\).
C. \(\frac{3}{8}\).
D. \(\frac{1}{4}\).
Phương pháp giải:
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết:
Các kết quả có thể của hành động gieo đồng xu của Sơn là S, N và của Minh là (S, S); (N, S); (S, N); (N, N).
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng sau:
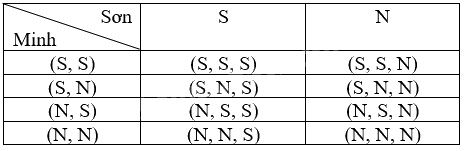
Số phần tử của không gian mẫu là 8. 8 kết quả này là đồng khả năng.
Có 3 kết quả thuận lợi của biến cố “Có đúng một đồng xu xuất hiện mặt ngửa” là: (S, S, N), (S, N, S), (N, S, S).
Vậy xác suất của biến cố “Có đúng một đồng xu xuất hiện mặt ngửa” là: \(\frac{3}{8}\).
Chọn C
Trả lời Câu 2 trang 74 Vở thực hành Toán 9
Gieo con xúc xắc cân đối liên tiếp hai lần. Xác suất để trong hai lần gieo số chấm xuất hiện trên con xúc xắc đều là số nguyên tố là
A. \(\frac{7}{{36}}\).
B. \(\frac{8}{{35}}\).
C. \(\frac{3}{8}\).
D. \(\frac{2}{9}\).
Phương pháp giải:
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết:
Kết quả của phép thử là cặp số (a, b) trong đó a và b tương ứng là số chấm trên con xúc xắc 1 và xúc xắc 2.
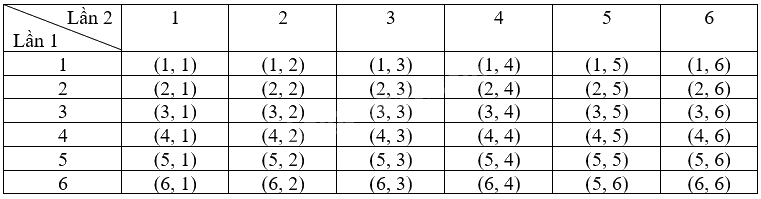Do đó, không gian mẫu có 36 phần tử, 36 kết quả có thể này là đồng khả năng
Có 9 kết quả thuận lợi của biến cố “Số chấm xuất hiện trên con xúc xắc trong hai lần gieo đều là số nguyên tố” là: (2, 2), (3, 2), (5, 2), (2, 3), (3, 3), (5, 3), (2, 5), (3, 5), (5, 5).
Xác suất của biến cố “Số chấm xuất hiện trên con xúc xắc trong hai lần gieo đều là số nguyên tố” là: \(\frac{9}{{36}} = \frac{1}{4}\).
Không có đáp án đúng
Trang 74 Vở thực hành Toán 9 tập 2 thường chứa các bài tập trắc nghiệm liên quan đến các chủ đề đã học trong chương. Việc nắm vững kiến thức lý thuyết và kỹ năng giải bài tập là yếu tố then chốt để đạt kết quả tốt. Bài viết này sẽ cung cấp lời giải chi tiết cho từng câu hỏi trắc nghiệm, đồng thời phân tích phương pháp giải và những lưu ý quan trọng.
Đề bài: (Nêu đề bài câu hỏi trắc nghiệm)
Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và định lý liên quan). Ví dụ: Để giải câu hỏi này, ta sử dụng công thức... Ta có: ... Vậy đáp án là...
Đề bài: (Nêu đề bài câu hỏi trắc nghiệm)
Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và định lý liên quan). Ví dụ: Câu này đòi hỏi chúng ta phải hiểu rõ về... Ta áp dụng định lý... Do đó, kết quả là...
Đề bài: (Nêu đề bài câu hỏi trắc nghiệm)
Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và định lý liên quan). Ví dụ: Để tìm ra đáp án chính xác, ta cần phân tích kỹ đề bài và loại trừ các phương án sai. Ta thấy rằng...
Việc giải các câu hỏi trắc nghiệm trang 74 Vở thực hành Toán 9 tập 2 không chỉ giúp bạn củng cố kiến thức mà còn rèn luyện kỹ năng làm bài thi trắc nghiệm. Đây là một kỹ năng quan trọng trong các kỳ thi quan trọng như thi vào lớp 10, thi học kỳ và thi quốc gia.
| Công thức/Định lý | Nội dung |
|---|---|
| Công thức nghiệm của phương trình bậc hai | x = (-b ± √(b² - 4ac)) / 2a |
| Định lý Pitago | a² + b² = c² |
| Hệ số góc của đường thẳng | k = tan α |
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải các câu hỏi trắc nghiệm trang 74 Vở thực hành Toán 9 tập 2 một cách hiệu quả. Chúc bạn học tập tốt và đạt kết quả cao trong các kỳ thi!
