Bài 13 trang 136, 137 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này thường liên quan đến các kiến thức về hàm số bậc nhất và ứng dụng của chúng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 13 này, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho tam giác ABC (left( {AB < AC} right)) ngoại tiếp đường tròn (I) với các tiếp điểm BC, CA, AB lần lượt là D, E, F. Gọi X và Y lần lượt là chân đường cao kẻ từ B và C xuống CI và BI. Chứng minh rằng: a) DBXF, DCYE là các tứ giác nội tiếp. b) Bốn điểm X, Y, E, F thẳng hàng.
Đề bài
Cho tam giác ABC \(\left( {AB < AC} \right)\) ngoại tiếp đường tròn (I) với các tiếp điểm BC, CA, AB lần lượt là D, E, F. Gọi X và Y lần lượt là chân đường cao kẻ từ B và C xuống CI và BI. Chứng minh rằng:
a) DBXF, DCYE là các tứ giác nội tiếp.
b) Bốn điểm X, Y, E, F thẳng hàng.
Phương pháp giải - Xem chi tiết
a) Vì \(\widehat {IXB} = \widehat {IDB} = \widehat {IFB} = {90^0}\) và \(\widehat {IYC} = \widehat {IDC} = \widehat {IEC} = {90^0}\) nên \(D,B,X,F,I\) cùng thuộc một đường tròn và \(D,C,Y,E,I\) cùng thuộc một đường tròn. Suy ra DBXF và DCYE là các tứ giác nội tiếp.
b) + \(\widehat {IXB} = \widehat {IYC} = {90^0}\) nên BXYC là tứ giác nội tiếp. Suy ra \(\widehat {YXC} = \widehat {YBC} = \widehat {IBF} = \widehat {IXF}.\) Suy ra X, F, Y thẳng hàng.
+ Chứng minh tương tự ta có X, E, Y thẳng hàng. Vậy ta có X, E, F, Y thẳng hàng
Lời giải chi tiết
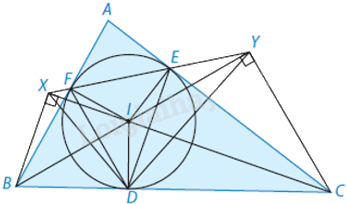
a) Ta có \(\widehat {IXB} = \widehat {IDB} = \widehat {IFB} = {90^0}\) và \(\widehat {IYC} = \widehat {IDC} = \widehat {IEC} = {90^0}\) nên \(D,B,X,F,I\) cùng thuộc một đường tròn và \(D,C,Y,E,I\) cùng thuộc một đường tròn. Suy ra DBXF và DCYE là các tứ giác nội tiếp.
b) Ta có \(\widehat {IXB} = \widehat {IYC} = {90^0}\) nên BXYC là tứ giác nội tiếp. Suy ra \(\widehat {YXC} = \widehat {YBC} = \widehat {IBF} = \widehat {IXF}.\)
Nên X, F, Y thẳng hàng. Tương tự X, E, Y thẳng hàng. Vậy ta có X, F, E, Y thẳng hàng.
Bài 13 trong Vở thực hành Toán 9 tập 2 tập trung vào việc vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Cụ thể, bài tập yêu cầu học sinh xác định hàm số, tìm hệ số góc và tung độ gốc, cũng như phân tích các yếu tố ảnh hưởng đến sự biến thiên của hàm số.
Bài 13 bao gồm các câu hỏi và bài tập nhỏ, được chia thành các phần khác nhau. Mỗi phần tập trung vào một khía cạnh cụ thể của hàm số bậc nhất. Dưới đây là phân tích chi tiết từng phần:
Câu hỏi này yêu cầu học sinh xác định xem một biểu thức đại số có phải là hàm số bậc nhất hay không. Để làm được điều này, học sinh cần nắm vững định nghĩa của hàm số bậc nhất, đó là hàm số có dạng y = ax + b, trong đó a và b là các số thực và a khác 0.
Câu hỏi này yêu cầu học sinh tìm hệ số góc (a) và tung độ gốc (b) của một hàm số bậc nhất cho trước. Hệ số góc cho biết độ dốc của đường thẳng biểu diễn hàm số, trong khi tung độ gốc là tọa độ giao điểm của đường thẳng với trục tung.
Câu hỏi này yêu cầu học sinh phân tích sự biến thiên của hàm số bậc nhất, tức là xác định xem hàm số đồng biến hay nghịch biến. Hàm số đồng biến khi hệ số góc a > 0, và nghịch biến khi hệ số góc a < 0.
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, học sinh cần:
Xét hàm số y = 2x + 3. Đây là một hàm số bậc nhất với hệ số góc a = 2 và tung độ gốc b = 3. Vì a > 0, hàm số đồng biến. Điều này có nghĩa là khi x tăng, y cũng tăng.
Để củng cố kiến thức, các em học sinh có thể tự giải các bài tập sau:
Bài 13 trang 136, 137 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc nhất và ứng dụng của chúng. Bằng cách nắm vững kiến thức và luyện tập thường xuyên, các em học sinh có thể tự tin giải quyết các bài tập tương tự.
| Khái niệm | Định nghĩa |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, với a ≠ 0 |
| Hệ số góc | Số a trong hàm số y = ax + b |
| Tung độ gốc | Số b trong hàm số y = ax + b |
| Hàm số đồng biến | Hàm số mà khi x tăng thì y cũng tăng (a > 0) |
| Hàm số nghịch biến | Hàm số mà khi x tăng thì y giảm (a < 0) |