Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 8 trang 105, 106 Vở thực hành Toán 9 tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, đầy đủ và kèm theo các giải thích chi tiết để bạn có thể hiểu rõ bản chất của bài toán.
Cho ngũ giác đều ABCDE có các cạnh bằng 4cm nội tiếp một đường tròn (O). a) Tính bán kính của (O) biết rằng ta lấy (cos {54^o} approx 0,59). b) Liệt kê năm phép quay ngược chiều giữ nguyên ngũ giác đều ABCDE.
Đề bài
Cho ngũ giác đều ABCDE có các cạnh bằng 4cm nội tiếp một đường tròn (O).
a) Tính bán kính của (O) biết rằng ta lấy \(\cos {54^o} \approx 0,59\).
b) Liệt kê năm phép quay ngược chiều giữ nguyên ngũ giác đều ABCDE.
Phương pháp giải - Xem chi tiết
a) + Nhận thấy $\overset\frown{AB}=\overset\frown{BC}=\overset\frown{CD}=\overset\frown{DE}=\overset\frown{EA}$, từ đó tính được góc AOB.
+ Gọi M là trung điểm của AB. Chứng minh OM vuông góc với AB và OM là tia phân giác của góc AOB, từ đó tính được góc AOM và góc MAO.
+ Bán kính của (O) là \(R = \frac{{AM}}{{\cos \widehat {MAO}}}\).
b) Phép quay ngược chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
Lời giải chi tiết
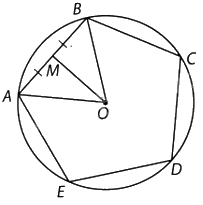
a) Ta thấy các cung nhỏ sau thỏa mãn: $\overset\frown{AB}=\overset\frown{BC}=\overset\frown{CD}=\overset\frown{DE}=\overset\frown{EA}$. Suy ra $\widehat{AOB}=sđ\overset\frown{AB}=\frac{{{360}^{o}}}{5}={{72}^{o}}$.
Gọi M là trung điểm của AB. Vì tam giác AOB cân tại O nên OM vuông góc với AB và OM là tia phân giác của góc AOB. Suy ra: \(\widehat {AOM} = \frac{{\widehat {AOB}}}{2} = \frac{{{{72}^o}}}{2} = {36^o}\).
Như vậy \(\widehat {MAO} = {90^o} - \widehat {AOM} = {54^o}\)
Bán kính của (O) là: \(R = \frac{{AM}}{{\cos \widehat {MAO}}} = \frac{{AM}}{{\cos {{54}^o}}} \approx \frac{2}{{0,59}} \approx 3,39\left( {cm} \right)\).
b) Năm phép quay ngược chiều giữ nguyên ngũ giác đều là các phép quay ngược chiều lần lượt \({72^{\rm{o}}},\,\,{144^{\rm{o}}},\) \({216^{\rm{o}}},\,\,{288^{\rm{o}}},\,\,{360^{\rm{o}}}\) với tâm O.
Bài 8 trang 105, 106 Vở thực hành Toán 9 tập 2 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số, bao gồm việc xác định hệ số góc, đường thẳng song song, và ứng dụng hàm số vào các bài toán hình học.
Bài 8 bao gồm các dạng bài tập sau:
Bài 8.1: Cho hàm số y = (m-1)x + 2. Tìm giá trị của m để hàm số đồng biến.
Lời giải: Hàm số y = (m-1)x + 2 là hàm số bậc nhất. Để hàm số đồng biến, hệ số góc m-1 phải lớn hơn 0. Vậy, m-1 > 0, suy ra m > 1.
Bài 8.2: Cho hai đường thẳng d1: y = 2x - 1 và d2: y = -x + 3. Xác định góc giữa hai đường thẳng.
Lời giải: Gọi α là góc giữa hai đường thẳng d1 và d2. Ta có tan α = |(a1 - a2) / (1 + a1 * a2)|, với a1 = 2 và a2 = -1. Vậy, tan α = |(2 - (-1)) / (1 + 2 * (-1))| = |3 / (-1)| = 3. Suy ra α = arctan(3) ≈ 71.57 độ.
Bài 8.3: Trong mặt phẳng tọa độ Oxy, cho A(1; 2) và B(3; 4). Viết phương trình đường thẳng AB.
Lời giải: Hệ số góc của đường thẳng AB là (yB - yA) / (xB - xA) = (4 - 2) / (3 - 1) = 2 / 2 = 1. Phương trình đường thẳng AB có dạng y = x + b. Thay tọa độ điểm A(1; 2) vào phương trình, ta có 2 = 1 + b, suy ra b = 1. Vậy, phương trình đường thẳng AB là y = x + 1.
Để học tốt hơn về hàm số bậc nhất, bạn có thể tham khảo các tài liệu sau:
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 8 trang 105, 106 Vở thực hành Toán 9 tập 2. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!