Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 77, 78 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Có hai túi đựng các tấm thẻ. Túi I đựng 4 tấm thẻ ghi các chữ cái TT, TH, HT và HH. Túi II đựng 2 tấm thẻ ghi các chữ cái T và H. Từ mỗi túi rút ngẫu nhiên ra một tấm thẻ rồi ghép hai thẻ lại với nhau để được ba chữ cái, trong đó thẻ hai chữ cái đặt trước, chẳng hạn tấm thẻ TT ghép với tấm thẻ H được ba chữ cái T TH. Tính xác suất của các biến cố sau: a) E: “Trong ba chữ cái, có hai chữ H và một chữ T”; b) F: “Trong ba chữ cái, có nhiều nhất hai chữ T”.
Đề bài
Có hai túi đựng các tấm thẻ. Túi I đựng 4 tấm thẻ ghi các chữ cái TT, TH, HT và HH. Túi II đựng 2 tấm thẻ ghi các chữ cái T và H. Từ mỗi túi rút ngẫu nhiên ra một tấm thẻ rồi ghép hai thẻ lại với nhau để được ba chữ cái, trong đó thẻ hai chữ cái đặt trước, chẳng hạn tấm thẻ TT ghép với tấm thẻ H được ba chữ cái T TH. Tính xác suất của các biến cố sau:
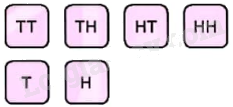
a) E: “Trong ba chữ cái, có hai chữ H và một chữ T”;
b) F: “Trong ba chữ cái, có nhiều nhất hai chữ T”.
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
Ta lập bảng sau:

Mỗi ô trong bảng là một kết quả có thể. Không gian mẫu\(\Omega = \left\{ {TTT;THT;HTT;TTH;THH;HTH;HHT;HHH} \right\}\). Có 8 kết quả có thể là đồng khả năng.
a) Có 3 kết quả thuận lợi cho biến cố E là THH; HHT; HTH. Vậy \(P\left( E \right) = \frac{3}{8}\).
b) Có 7 kết quả thuận lợi của biến cố F là HHH; THT; THT; HTT; THH; HHT; HTH. Vậy \(P\left( F \right) = \frac{7}{8}\).
Bài 1 trang 77, 78 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình ôn tập về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này.
Trước khi đi vào giải bài tập, chúng ta cùng nhau ôn lại một số kiến thức cơ bản về hàm số bậc nhất:
Bài 1 thường bao gồm các dạng bài tập sau:
Ví dụ minh họa:
Giả sử bài tập yêu cầu xác định hàm số y = 2x + 3 có phải là hàm số bậc nhất hay không. Ta thấy rằng hàm số này có dạng y = ax + b, với a = 2 và b = 3. Vì a ≠ 0, nên hàm số y = 2x + 3 là hàm số bậc nhất.
Để củng cố kiến thức về hàm số bậc nhất, các em có thể luyện tập thêm các bài tập tương tự trong Vở thực hành Toán 9 tập 2 và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Ngoài các kiến thức cơ bản đã trình bày ở trên, các em có thể tìm hiểu thêm về các ứng dụng của hàm số bậc nhất trong các lĩnh vực khác nhau của đời sống và khoa học. Ví dụ, hàm số bậc nhất có thể được sử dụng để mô tả mối quan hệ giữa nhiệt độ và thời gian, giữa quãng đường và thời gian, giữa giá cả và số lượng sản phẩm, v.v.
Bảng tổng hợp các công thức quan trọng:
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| a | Hệ số góc |
| b | Giao điểm với trục Oy |
| -b/a | Giao điểm với trục Ox |
Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập này, các em sẽ hiểu rõ hơn về hàm số bậc nhất và có thể tự tin giải quyết các bài tập tương tự. Chúc các em học tập tốt!