Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 71 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải dễ hiểu, chi tiết từng bước, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Có hai nhóm học sinh: Nhóm I có ba học sinh nam là Huy, Sơn, Tùng; Nhóm II có ba học sinh nữ là Hồng, Phương, Linh. Giáo viên chọn ngẫu nhiên một học sinh từ mỗi nhóm. a) Phép thử và kết quả của phép thử là gì? b) Mô tả không gian mẫu của phép thử. Không gian mẫu có bao nhiêu phần tử?
Đề bài
Có hai nhóm học sinh: Nhóm I có ba học sinh nam là Huy, Sơn, Tùng; Nhóm II có ba học sinh nữ là Hồng, Phương, Linh. Giáo viên chọn ngẫu nhiên một học sinh từ mỗi nhóm.
a) Phép thử và kết quả của phép thử là gì?
b) Mô tả không gian mẫu của phép thử. Không gian mẫu có bao nhiêu phần tử?
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về phép thử để tìm phép thử: Một hoặc một số hành động, thực nghiệm được tiến hành liên tiếp hay đồng thời mà kết quả của chúng không thể biết được trước khi thực hiện nhưng có thể liệt kê các kết quả có thể xảy ra, được gọi là một phép thử ngẫu nhiên, gọi tắt là phép thử.
b) Sử dụng kiến thức về không gian mẫu để tìm không gian mẫu: Sử dụng kiến thức về không gian mẫu để tìm không gian mẫu: Tập hợp tất cả các kết quả có thể xảy ra của phép thử (gọi tắt là tập tất cả các kết quả có thể của phép thử) được gọi là không gian mẫu của phép thử.
Ta có thể tìm số phần tử của không gian mẫu bằng cách lập bảng.
Lời giải chi tiết
a) Phép thử là chọn ngẫu nhiên một học sinh từ mỗi nhóm.
Kết quả của phép thử là một cặp (a, b) trong đó a và b tương ứng là tên của một học sinh nhóm I và một học sinh Nhóm II.
b) Ta lập bảng sau:
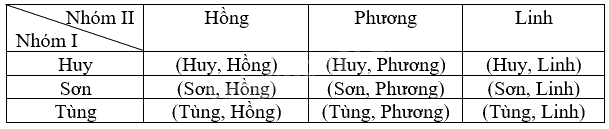
Không gian mẫu của phép thử $\Omega =${(Huy, Hồng); (Sơn, Hồng); (Huy, Phương); (Sơn, Phương); (Tùng, Phương) ; (Huy, Linh); (Tùng, Hồng) (Sơn, Linh); (Tùng, Linh)}.
Không gian mẫu có 9 phần tử.
Bài 3 trang 71 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong quá trình ôn tập chương hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất, bao gồm:
Để giải bài 3 trang 71 Vở thực hành Toán 9 tập 2 một cách hiệu quả, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán và lựa chọn phương pháp giải phù hợp. Thông thường, bài toán này sẽ yêu cầu học sinh:
Dưới đây là lời giải chi tiết bài 3 trang 71 Vở thực hành Toán 9 tập 2. Chúng tôi sẽ trình bày lời giải từng bước một, kèm theo các giải thích rõ ràng để giúp các em hiểu rõ hơn về cách giải bài toán này.
(a) Cho hàm số y = 2x + 3. Hãy xác định hệ số a và b của hàm số.
Lời giải:
Hàm số y = 2x + 3 là hàm số bậc nhất có dạng y = ax + b. So sánh với dạng tổng quát, ta có a = 2 và b = 3.
(b) Vẽ đồ thị của hàm số y = 2x + 3.
Lời giải:
Để vẽ đồ thị của hàm số y = 2x + 3, ta cần xác định hai điểm thuộc đồ thị. Ta có thể chọn x = 0 và x = 1 để tính giá trị tương ứng của y:
Nối hai điểm A(0; 3) và B(1; 5) bằng một đường thẳng, ta được đồ thị của hàm số y = 2x + 3.
(c) Tìm tọa độ giao điểm của đồ thị hàm số y = 2x + 3 với đường thẳng y = -x + 6.
Lời giải:
Để tìm tọa độ giao điểm của hai đường thẳng y = 2x + 3 và y = -x + 6, ta giải hệ phương trình sau:
| y = 2x + 3 | y = -x + 6 |
Thay y = 2x + 3 vào phương trình y = -x + 6, ta được:
2x + 3 = -x + 6
3x = 3
x = 1
Thay x = 1 vào phương trình y = 2x + 3, ta được:
y = 2(1) + 3 = 5
Vậy tọa độ giao điểm của hai đường thẳng là (1; 5).
Để củng cố kiến thức về hàm số bậc nhất, các em có thể làm thêm các bài tập tương tự sau:
Bài 3 trang 71 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp các em ôn tập và củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các giải thích rõ ràng trên đây, các em sẽ hiểu rõ hơn về cách giải bài toán này và tự tin giải các bài tập tương tự.