Bài 8 trang 127 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này thường liên quan đến các kiến thức về hàm số bậc nhất và ứng dụng của chúng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8 trang 127 VTH Toán 9 tập 2, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp những giải pháp học tập tốt nhất, hỗ trợ các em học sinh học tập hiệu quả và đạt kết quả cao.
Một chiếc kem ốc quế gồm hai phần: Phần phía dưới là một hình nón có chiều cao gấp đôi bán kính đáy, phần trên là một nửa hình cầu có đường kính bằng đường kính đáy của hình nón phía dưới. Thể tích phần kem phía trên bằng (200c{m^3}). Tính thể tích của cả chiếc kem.
Đề bài
Một chiếc kem ốc quế gồm hai phần: Phần phía dưới là một hình nón có chiều cao gấp đôi bán kính đáy, phần trên là một nửa hình cầu có đường kính bằng đường kính đáy của hình nón phía dưới. Thể tích phần kem phía trên bằng \(200c{m^3}\). Tính thể tích của cả chiếc kem.
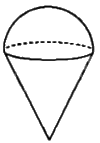
Phương pháp giải - Xem chi tiết
+ Ta có \({V_1} = \frac{1}{2}.\frac{4}{3}\pi {R^3} = 200\left( {c{m^3}} \right)\), từ đó tính được R.
+ Tính thể tích của phần kem phía dưới.
+ Thể tích chiếc kem bằng tổng thể tích phía trên và phía dưới chiếc kem.
Lời giải chi tiết
Thể tích phần kem phía trên là \(200c{m^3}\) nên:
\({V_1} = \frac{1}{2}.\frac{4}{3}\pi {R^3} = 200\left( {c{m^3}} \right)\),
suy ra \(R = \sqrt[3]{{\frac{{300}}{\pi }}}cm\).
Thể tích phần kem phía dưới là:
\({V_2} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {R^2}.2R \\= \frac{2}{3}\pi {R^3} = \frac{2}{3}\pi .\frac{{300}}{\pi } = 200\left( {c{m^3}} \right).\)
Thể tích cả chiếc kem là: \(200 + 200 = 400\left( {c{m^3}} \right)\).
Bài 8 trang 127 Vở thực hành Toán 9 tập 2 thường xoay quanh việc xác định hệ số góc và đường thẳng song song, vuông góc. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số bậc nhất, đặc biệt là phương trình đường thẳng và các tính chất liên quan.
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài 8 trang 127. Tuy nhiên, dựa trên các dạng bài tập thường gặp, chúng ta có thể đưa ra một ví dụ minh họa:
Ví dụ: Cho hai đường thẳng (d1): y = 2x + 3 và (d2): y = (m - 1)x + 2. Tìm giá trị của m để (d1) và (d2) song song.
Giải:
Để (d1) và (d2) song song, ta cần có:
Từ 2 = m - 1, ta suy ra m = 3. Vì 3 ≠ 2, điều kiện song song được thỏa mãn.
Vậy, m = 3.
Để nắm vững kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, học sinh nên luyện tập thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các nguồn tài liệu học tập khác. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập đa dạng, giúp các em củng cố kiến thức và tự tin hơn trong các kỳ thi.
Hy vọng với những hướng dẫn chi tiết và bài tập luyện tập trên, các em học sinh sẽ giải quyết thành công bài 8 trang 127 Vở thực hành Toán 9 tập 2 và đạt kết quả tốt trong môn Toán.