Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 118, 119 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất và ứng dụng của nó.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải bài tập Toán 9 một cách dễ hiểu, chi tiết, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tam giác ABC cân tại A, đường cao AH, có (AB = 5cm,BC = 8cm). Quay tam giác ABC một vòng quanh cạnh AH ta được một hình nón. a) Tính thể tích của hình nón (làm tròn kết quả đến hàng phần trăm của (c{m^3})). b) Tính diện tích toàn phần của hình nón (làm tròn kết quả đến hàng phần trăm của (c{m^2})).
Đề bài
Tam giác ABC cân tại A, đường cao AH, có \(AB = 5cm,BC = 8cm\). Quay tam giác ABC một vòng quanh cạnh AH ta được một hình nón.
a) Tính thể tích của hình nón (làm tròn kết quả đến hàng phần trăm của \(c{m^3}\)).
b) Tính diện tích toàn phần của hình nón (làm tròn kết quả đến hàng phần trăm của \(c{m^2}\)).
Phương pháp giải - Xem chi tiết
a) Thể tích của hình nón có bán kính đáy R và chiều cao h là: \(V={{S}_{đ\acute{a}y}}.h=\pi {{R}^{2}}h\).
b) Diện tích xung quanh của hình nón bán kính r và độ dài đường sinh l là: \({S_{xq}} = \pi rl\).
Diện tích toàn phần hình nón bằng diện tích xung quanh cộng với diện tích hai đáy.
Lời giải chi tiết
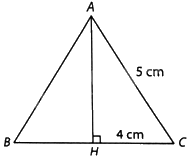
a) Tam giác ABC cân tại A, đường cao AH. Suy ra H là trung điểm của BC nên \(HC = HB = \frac{{BC}}{2} = 4cm\)
Tam giác AHC vuông tại H nên theo định lí Pythagore ta có:
\(A{H^2} + H{C^2} = A{C^2}\)
\(A{H^2} + {4^2} = {5^2}\)
\(A{H^2} = 25 - 16 = 9\)
\(AH = 3cm\).
Khi đó: \(R = 4cm,h = 3cm,l = 5cm\)
Thể tích của hình nón là: \(V=\frac{1}{3}{{S}_{đ\acute{a}y}}.h=\frac{1}{3}\pi {{R}^{2}}h=\frac{1}{3}\pi {{.4}^{2}}.3=16\pi \approx 50,27\left( c{{m}^{3}} \right)\)
b) Diện tích toàn phần của hình nón là: \({{S}_{tp}}={{S}_{xq}}+{{S}_{đ\acute{a}y}}=\pi Rl+\pi {{R}^{2}}=\pi .4.5+\pi {{.4}^{2}}=36\pi \approx 113,10\left( c{{m}^{2}} \right)\)
Bài 8 trang 118, 119 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình ôn tập về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất, bao gồm:
Bài 8 thường bao gồm các dạng bài tập sau:
Để giải bài 8 trang 118, 119 Vở thực hành Toán 9 tập 2 một cách hiệu quả, các em cần:
Bài tập: Cho hàm số y = 3x + 2. Tìm tọa độ giao điểm của đồ thị hàm số với trục Ox.
Giải:
Để tìm tọa độ giao điểm của đồ thị hàm số với trục Ox, ta cần giải phương trình 3x + 2 = 0.
Giải phương trình, ta được x = -2/3.
Vậy tọa độ giao điểm của đồ thị hàm số với trục Ox là (-2/3; 0).
Để củng cố kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa và vở bài tập Toán 9 tập 2.
Hy vọng với lời giải chi tiết và hướng dẫn giải bài 8 trang 118, 119 Vở thực hành Toán 9 tập 2, các em sẽ học tập tốt môn Toán 9 và đạt kết quả cao trong các kỳ thi.