Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 111 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và các bài tập luyện tập để nắm vững kiến thức.
Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp.
Đề bài
Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp
Phương pháp giải - Xem chi tiết
+ Chứng minh OP, ON, OM lần lượt là các đường cao của các tam giác AOB, AOC, BOC.
+ Tứ giác ANOP có \(\widehat {ANO} = \widehat {APO} = {90^0}\) nên tứ giác ANOP nội tiếp đường tròn có tâm là trung điểm của AO và bán kính bằng \(\frac{{AO}}{2}\).
+ Chứng minh tương tự ta có BPOM, CMON cũng là các tứ giác nội tiếp.
Lời giải chi tiết
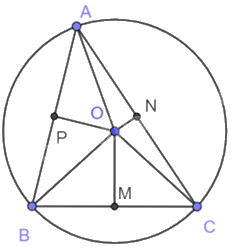
Do các tam giác AOB, AOC, BOC đều cân tại O nên OP, ON, OM lần lượt là các đường cao của các tam giác này.
Do vậy, tứ giác ANOP có \(\widehat {ANO} = \widehat {APO} = {90^0}\). Do vậy tứ giác ANOP nội tiếp đường tròn có tâm là trung điểm của AO và bán kính bằng \(\frac{{AO}}{2}\). Tương tự BPOM, CMON cũng là các tứ giác nội tiếp.
Bài 2 trang 111 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong quá trình ôn tập chương hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và các lưu ý quan trọng để các em có thể hiểu rõ và làm bài tốt nhất.
Bài 2 thường bao gồm các dạng bài tập sau:
Để giải bài 2 trang 111 Vở thực hành Toán 9 tập 2, các em cần nắm vững các kiến thức sau:
Ví dụ minh họa:
Giả sử bài tập yêu cầu xác định hệ số a của hàm số y = ax + 2 khi đường thẳng đi qua điểm A(1; 5). Ta thay tọa độ điểm A vào phương trình hàm số để tìm a:
5 = a * 1 + 2
=> a = 3
Vậy hàm số cần tìm là y = 3x + 2.
Ngoài việc áp dụng các kiến thức cơ bản, các em cũng cần rèn luyện kỹ năng giải các dạng bài tập khác nhau. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để giải dạng bài này, các em cần xác định các yếu tố đã biết (ví dụ: hệ số góc, điểm mà đồ thị đi qua) và sử dụng các công thức liên quan để tìm các yếu tố còn lại.
Để giải dạng bài này, các em thay giá trị đã biết vào phương trình hàm số và giải phương trình để tìm giá trị còn lại.
Để giải dạng bài này, các em giải hệ phương trình tương ứng với hai đường thẳng đó. Nghiệm của hệ phương trình là tọa độ giao điểm của hai đường thẳng.
Để củng cố kiến thức, các em có thể làm thêm các bài tập sau:
Bài 2 trang 111 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp các em ôn tập và củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các lưu ý trên, các em sẽ tự tin giải bài tập và đạt kết quả tốt nhất. Chúc các em học tập tốt!