Bài 8 trang 101 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này thường liên quan đến các kiến thức về hàm số bậc nhất và ứng dụng của chúng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8 trang 101 VTH Toán 9 tập 2, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp những giải pháp học tập tốt nhất, hỗ trợ các em học sinh học tập hiệu quả và đạt kết quả cao.
Cho tam giác nhọn ABC có các đường cao BE, CF cắt nhau tại H. Chứng minh rằng: a) (widehat {EFH} = widehat {HBC},widehat {FEH} = widehat {HCB}); b) (widehat {BHF} = widehat {BAC} = widehat {CHE}).
Đề bài
Cho tam giác nhọn ABC có các đường cao BE, CF cắt nhau tại H. Chứng minh rằng:
a) \(\widehat {EFH} = \widehat {HBC},\widehat {FEH} = \widehat {HCB}\);
b) \(\widehat {BHF} = \widehat {BAC} = \widehat {CHE}\).
Phương pháp giải - Xem chi tiết
a) + Chứng minh các tam giác vuông BFC và BEC cùng nội tiếp đường tròn đường kính BC nên tứ giác BCEF nội tiếp đường tròn đường kính BC. Từ đó suy ra \(\widehat {EFC} = \widehat {EBC}\).
+ Chứng minh tương tự ta có: \(\widehat {FEH} = \widehat {HCB}\).
b) + Chứng minh các tam giác vuông AEH và AFH cùng nội tiếp đường tròn đường kính AH nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
+ Chứng minh \(\widehat {EHF} + \widehat {EAF} = {180^o}\), suy ra \(\widehat {BHF} = {180^o} - \widehat {EHF} = \widehat {EAF} = \widehat {BAC}\).
+ Chứng minh tương tự ta có: \(\widehat {CHE} = \widehat {BAC}\).
Lời giải chi tiết
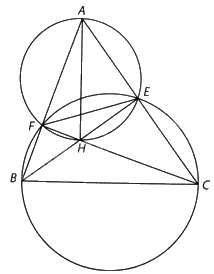
a) Ta có: \(\widehat {BFC} = \widehat {BEC} = {90^o}\). Do vậy các tam giác vuông BFC và BEC cùng nội tiếp đường tròn đường kính BC.
Suy ra, tứ giác BCEF nội tiếp đường tròn đường kính BC. Vì \(\widehat {EFC}\) và \(\widehat {EBC}\) là hai góc nội tiếp đường tròn ngoại tiếp của tứ giác này và cùng chắn cung CE nên \(\widehat {EFC} = \widehat {EBC}\). Suy ra \(\widehat {EFH} = \widehat {EFC} = \widehat {EBC} = \widehat {HBC}\).
Tương tự ta có: \(\widehat {FEH} = \widehat {HCB}\).
b) Ta có: \(\widehat {AEH} = \widehat {AFH} = {90^o}\). Do vậy các tam giác vuông AEH và AFH cùng nội tiếp đường tròn đường kính AH.
Suy ra, tứ giác AEHF nội tiếp đường tròn đường kính AH. Vì góc FAE và góc FHE là hai góc đối của tứ giác nội tiếp AEHF nên \(\widehat {EHF} + \widehat {EAF} = {180^o}\).
Suy ra \(\widehat {BHF} = {180^o} - \widehat {EHF} = \widehat {EAF} = \widehat {BAC}\).
Tương tự ta có: \(\widehat {CHE} = \widehat {BAC}\).
Vậy \(\widehat {BHF} = \widehat {BAC} = \widehat {CHE}\).
Bài 8 trang 101 Vở thực hành Toán 9 tập 2 thường xoay quanh việc xác định hệ số góc và đường thẳng song song, vuông góc. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số bậc nhất, đặc biệt là phương trình đường thẳng và các tính chất liên quan.
Trước khi bắt tay vào giải bài tập, hãy đọc kỹ đề bài và xác định yêu cầu chính. Thông thường, bài toán sẽ yêu cầu:
(Giả sử bài 8 có nội dung: Cho đường thẳng d: y = 2x - 3. Hãy tìm phương trình đường thẳng d' song song với d và đi qua điểm A(1; 2).)
Lời giải:
Ngoài dạng bài tập tìm phương trình đường thẳng song song, vuông góc, học sinh còn có thể gặp các dạng bài tập sau:
Để nắm vững kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, học sinh nên:
Hàm số bậc nhất là nền tảng cho việc học các kiến thức nâng cao hơn về hàm số trong chương trình Toán học. Việc nắm vững kiến thức về hàm số bậc nhất sẽ giúp học sinh dễ dàng tiếp thu các khái niệm mới và giải quyết các bài toán phức tạp hơn.
Giaitoan.edu.vn hy vọng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin hơn trong việc giải bài 8 trang 101 Vở thực hành Toán 9 tập 2 và các bài tập tương tự. Chúc các em học tập tốt!