Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 114 Vở thực hành Toán 9. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải dễ hiểu, chi tiết từng bước, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F. a) Chứng minh rằng chu vi của tam giác SEF=SA+SB. b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng (SE = SF).
Đề bài
Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F.
a) Chứng minh rằng chu vi của tam giác SEF=SA+SB.
b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng \(SE = SF\).
Phương pháp giải - Xem chi tiết
a) + Theo tính chất hai tiếp tuyến cắt nhau suy ra \(EA = ME\), \(FB = FM\).
+ Chu vi của \(\Delta \)SEF là:
\({P_{SEF}} = SE + EF + SF = SE + ME + MF + SF = \left( {SE + EA} \right) + \left( {FB + SF} \right) = SA + SB\).
b) + Theo tính chất hai tiếp tuyến cắt nhau suy ra \(SA = SB\) và SO là tia phân giác của góc ASB.
+ Chứng minh SAB cân tại S nên SO là đường phân giác nên đồng thời là đường cao suy ra \(SO \bot AB\).
+ Chứng minh EF//AB.
+ Chứng minh \(\frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\), mà \(SA = SB\), do đó \(SE = SF\)
Lời giải chi tiết
(H.5.31)
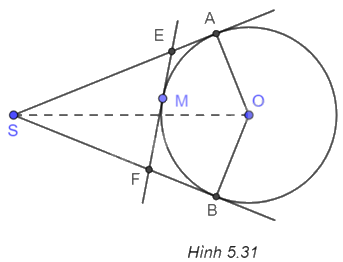
a) Xét hai tiếp tuyến của (O) cắt nhau tại E ta có \(EA = ME\). Tương tự, có \(FB = FM\).
Chu vi của tam giác SEF là
\({P_{SEF}} = SE + EF + SF = SE + ME + MF + SF = SE + EA + FB + SF\)
\( = \left( {SE + EA} \right) + \left( {FB + SF} \right) = SA + SB\) (điều phải chứng minh)
b) Giả sử M trùng với giao điểm của SO và (O).
Xét hai tiếp tuyến SA, SB của (O) cắt nhau tại S, ta có \(SA = SB\) và SO là tia phân giác của góc ASB.
Tam giác SAB cân tại S (do \(SA = SB\)) có SO là đường phân giác nên đồng thời là đường cao của tam giác, tức là \(SO \bot AB\).
EF là tiếp tuyến của (O) tại M nên \(EF \bot SO\).
Từ đó suy ra EF//AB (cùng vuông góc với SO).
Tam giác SAB có EF//AB nên \(\frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\), mà \(SA = SB\), do đó \(SE = SF\) (điều phải chứng minh)
Bài 4 trang 114 Vở thực hành Toán 9 là một bài tập quan trọng trong chương trình ôn tập về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về hàm số bậc nhất, bao gồm:
Bài 4 trang 114 Vở thực hành Toán 9 thường yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:
Cho hàm số y = 2x - 3. Hãy xác định hệ số góc và tung độ gốc của hàm số.
Lời giải:
Hệ số góc của hàm số là a = 2.
Tung độ gốc của hàm số là b = -3.
Vẽ đồ thị hàm số y = -x + 1.
Lời giải:
Để vẽ đồ thị hàm số, ta cần xác định hai điểm thuộc đồ thị. Chọn x = 0, ta có y = 1. Chọn x = 1, ta có y = 0. Vậy, đồ thị hàm số đi qua hai điểm A(0; 1) và B(1; 0). Nối hai điểm này lại, ta được đồ thị hàm số.
Tìm tọa độ giao điểm của đồ thị hàm số y = 3x + 2 với trục Ox.
Lời giải:
Giao điểm của đồ thị hàm số với trục Ox là điểm có tung độ y = 0. Thay y = 0 vào phương trình hàm số, ta có:
0 = 3x + 2
Giải phương trình, ta được x = -2/3.
Vậy, tọa độ giao điểm của đồ thị hàm số với trục Ox là (-2/3; 0).
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, các em nên:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Bài 4 trang 114 Vở thực hành Toán 9 là một bài tập quan trọng giúp các em học sinh ôn tập và củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, các em sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.