Bạn đang gặp khó khăn trong việc giải các bài tập trắc nghiệm Toán 9 trang 97 và 98 trong Vở thực hành? giaitoan.edu.vn là địa chỉ tin cậy, cung cấp đáp án chi tiết và lời giải dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi hiểu rằng việc làm bài tập trắc nghiệm đòi hỏi sự chính xác và nhanh nhạy. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn bộ giải đáp đầy đủ, giúp bạn tiết kiệm thời gian và đạt kết quả tốt nhất.
Cho tam giác ABC vuông tại A. Tâm đường tròn đi qua ba đỉnh của tam giác ABC là A. trung điểm của BC. B. trung điểm của AC. C. trung điểm của AB. D. trọng tâm của tam giác ABC.
Trả lời Câu 4 trang 98 Vở thực hành Toán 9
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn?
A. Đường tròn không có trục đối xứng.
B. Đường tròn có duy nhất một trục đối xứng là đường kính.
C. Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau.
D. Đường tròn có vô số trục đối xứng là đường kính.
Phương pháp giải:
Đường tròn có vô số trục đối xứng là đường kính.
Lời giải chi tiết:
Đường tròn có vô số trục đối xứng là đường kính.
Chọn D
Trả lời Câu 1 trang 97 Vở thực hành Toán 9
Cho tam giác ABC vuông tại A. Tâm đường tròn đi qua ba đỉnh của tam giác ABC là
A. trung điểm của BC.
B. trung điểm của AC.
C. trung điểm của AB.
D. trọng tâm của tam giác ABC.
Phương pháp giải:
+ Gọi O là trung điểm của BC.
+ Chứng minh \(OA = OB = OC\), suy ra O là tâm đường tròn đi qua ba đỉnh của tam giác ABC.
Lời giải chi tiết:
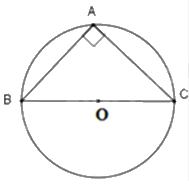
Gọi O là trung điểm của BC.
Tam giác ABC vuông tại A, có AO là đường trung tuyến nên \(OA = OB = OC\). Do đó, O là tâm đường tròn đi qua ba đỉnh của tam giác ABC.
Vậy tâm đường tròn đi qua ba đỉnh của tam giác ABC vuông tại A là trung điểm của BC.
Chọn A
Trả lời Câu 2 trang 97 Vở thực hành Toán 9
Trên mặt phẳng tọa độ Oxy, cho các điểm A(-1; -1), B(-1; -2), C\(\left( {\sqrt 2 ;\sqrt 2 } \right)\) và đường tròn tâm O bán kính 2cm. Khẳng định nào sau đây là sai?
A. Điểm A nằm trong đường tròn (O; 2).
B. Điểm B nằm trên đường tròn (O; 2).
C. Điểm C nằm trên đường tròn (O; 2).
D. Điểm B nằm ngoài đường tròn (O; 2).
Phương pháp giải:
Biểu diễn các điểm và đường tròn (O) trên mặt phẳng tọa độ rồi tìm đáp án đúng.
Lời giải chi tiết:
Biểu diễn các điểm và đường tròn (O) trên mặt phẳng tọa độ ta có:
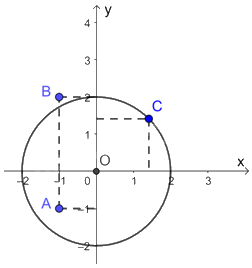
Nhìn vào hình vẽ ta thấy, điểm B nằm ngoài đường tròn (O; 2), điểm A nằm trong đường tròn (O; 2), điểm C nằm trên đường tròn (O; 2).
Chọn B
Trả lời Câu 3 trang 98 Vở thực hành Toán 9
Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H. Khẳng định nào sau đây là đúng?
A. Bốn điểm B, E, D, C cùng nằm trên một đường tròn.
B. Bốn điểm A, E, H, D cùng nằm trên một đường tròn.
C. \(DE < BC\).
D. Cả ba đáp án trên đều đúng.
Phương pháp giải:
+ Gọi G, K lần lượt là trung điểm của AH, BC.
+ Chứng minh \(GA = GE = GD = GH\) nên bốn điểm A, E, H, D thuộc đường tròn tâm (G, GA).
+ Chứng minh \(KB = KD = KE = KC\) nên bốn điểm B, E, D, C thuộc đường tròn tâm (K, KC).
+ Sử dụng quan hệ giữa cạnh và góc trong tam giác chứng minh được \(DE < BC\).
Lời giải chi tiết:
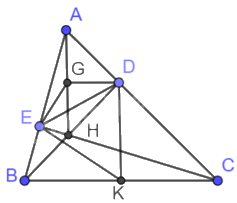
Gọi G, K lần lượt là trung điểm của AH, BC.
Vì EG là đường trung tuyến trong tam giác AEH vuông tại E nên \(EG = GH = AG\).
Vì DG là đường trung tuyến trong tam giác ADH vuông tại D nên \(DG = GH = AG\).
Do đó \(GA = GE = GD = GH\) nên bốn điểm A, E, H, D thuộc đường tròn tâm (G, GA).
Vì EK là đường trung tuyến trong tam giác BEC vuông tại E nên \(EK = BK = KC\).
Vì DK là đường trung tuyến trong tam giác BDC vuông tại D nên \(DK = BK = KC\).
Do đó \(KB = KD = KE = KC\) nên bốn điểm B, E, D, C thuộc đường tròn tâm (K, KC).
Tam giác EDC có góc EDC là góc tù nên \(ED < EC\) (quan hệ giữa cạnh và góc đối diện trong tam giác)
Tam giác BEC vuông tại E nên \(EC < BC\) (quan hệ giữa cạnh và góc đối diện trong tam giác)
Do đó, \(DE < BC\)
Chọn D
Chọn phương án đúng trong mỗi câu sau:
Trả lời Câu 1 trang 97 Vở thực hành Toán 9
Cho tam giác ABC vuông tại A. Tâm đường tròn đi qua ba đỉnh của tam giác ABC là
A. trung điểm của BC.
B. trung điểm của AC.
C. trung điểm của AB.
D. trọng tâm của tam giác ABC.
Phương pháp giải:
+ Gọi O là trung điểm của BC.
+ Chứng minh \(OA = OB = OC\), suy ra O là tâm đường tròn đi qua ba đỉnh của tam giác ABC.
Lời giải chi tiết:
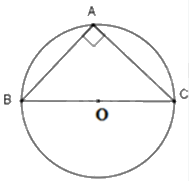
Gọi O là trung điểm của BC.
Tam giác ABC vuông tại A, có AO là đường trung tuyến nên \(OA = OB = OC\). Do đó, O là tâm đường tròn đi qua ba đỉnh của tam giác ABC.
Vậy tâm đường tròn đi qua ba đỉnh của tam giác ABC vuông tại A là trung điểm của BC.
Chọn A
Trả lời Câu 2 trang 97 Vở thực hành Toán 9
Trên mặt phẳng tọa độ Oxy, cho các điểm A(-1; -1), B(-1; -2), C\(\left( {\sqrt 2 ;\sqrt 2 } \right)\) và đường tròn tâm O bán kính 2cm. Khẳng định nào sau đây là sai?
A. Điểm A nằm trong đường tròn (O; 2).
B. Điểm B nằm trên đường tròn (O; 2).
C. Điểm C nằm trên đường tròn (O; 2).
D. Điểm B nằm ngoài đường tròn (O; 2).
Phương pháp giải:
Biểu diễn các điểm và đường tròn (O) trên mặt phẳng tọa độ rồi tìm đáp án đúng.
Lời giải chi tiết:
Biểu diễn các điểm và đường tròn (O) trên mặt phẳng tọa độ ta có:
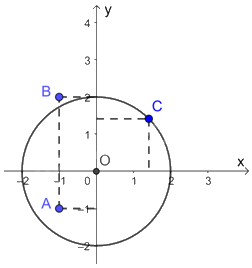
Nhìn vào hình vẽ ta thấy, điểm B nằm ngoài đường tròn (O; 2), điểm A nằm trong đường tròn (O; 2), điểm C nằm trên đường tròn (O; 2).
Chọn B
Trả lời Câu 3 trang 98 Vở thực hành Toán 9
Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H. Khẳng định nào sau đây là đúng?
A. Bốn điểm B, E, D, C cùng nằm trên một đường tròn.
B. Bốn điểm A, E, H, D cùng nằm trên một đường tròn.
C. \(DE < BC\).
D. Cả ba đáp án trên đều đúng.
Phương pháp giải:
+ Gọi G, K lần lượt là trung điểm của AH, BC.
+ Chứng minh \(GA = GE = GD = GH\) nên bốn điểm A, E, H, D thuộc đường tròn tâm (G, GA).
+ Chứng minh \(KB = KD = KE = KC\) nên bốn điểm B, E, D, C thuộc đường tròn tâm (K, KC).
+ Sử dụng quan hệ giữa cạnh và góc trong tam giác chứng minh được \(DE < BC\).
Lời giải chi tiết:
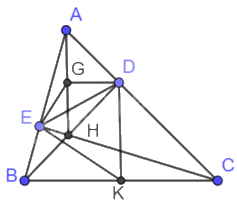
Gọi G, K lần lượt là trung điểm của AH, BC.
Vì EG là đường trung tuyến trong tam giác AEH vuông tại E nên \(EG = GH = AG\).
Vì DG là đường trung tuyến trong tam giác ADH vuông tại D nên \(DG = GH = AG\).
Do đó \(GA = GE = GD = GH\) nên bốn điểm A, E, H, D thuộc đường tròn tâm (G, GA).
Vì EK là đường trung tuyến trong tam giác BEC vuông tại E nên \(EK = BK = KC\).
Vì DK là đường trung tuyến trong tam giác BDC vuông tại D nên \(DK = BK = KC\).
Do đó \(KB = KD = KE = KC\) nên bốn điểm B, E, D, C thuộc đường tròn tâm (K, KC).
Tam giác EDC có góc EDC là góc tù nên \(ED < EC\) (quan hệ giữa cạnh và góc đối diện trong tam giác)
Tam giác BEC vuông tại E nên \(EC < BC\) (quan hệ giữa cạnh và góc đối diện trong tam giác)
Do đó, \(DE < BC\)
Chọn D
Trả lời Câu 4 trang 98 Vở thực hành Toán 9
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn?
A. Đường tròn không có trục đối xứng.
B. Đường tròn có duy nhất một trục đối xứng là đường kính.
C. Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau.
D. Đường tròn có vô số trục đối xứng là đường kính.
Phương pháp giải:
Đường tròn có vô số trục đối xứng là đường kính.
Lời giải chi tiết:
Đường tròn có vô số trục đối xứng là đường kính.
Chọn D
Trang 97 và 98 Vở thực hành Toán 9 tập trung vào các chủ đề quan trọng như hệ phương trình bậc hai, phương trình quy về bậc hai, và ứng dụng của phương trình bậc hai trong giải toán thực tế. Việc nắm vững kiến thức này là nền tảng cho các chương trình học tiếp theo.
Trước khi đi vào giải chi tiết, chúng ta cần nắm vững nội dung chính của hai trang này. Trang 97 thường tập trung vào việc ôn tập các kiến thức cơ bản về hệ phương trình bậc hai, các phương pháp giải hệ phương trình như phương pháp thế, phương pháp cộng đại số. Trang 98 tiếp tục đào sâu vào các bài tập ứng dụng, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề thực tế.
Dưới đây là giải chi tiết các câu hỏi trắc nghiệm trang 97 và 98 Vở thực hành Toán 9:
...(Tiếp tục giải chi tiết các câu hỏi còn lại)...
Để giải bài tập trắc nghiệm Toán 9 hiệu quả, bạn có thể áp dụng một số mẹo sau:
Phương trình bậc hai không chỉ là một kiến thức lý thuyết mà còn có ứng dụng rộng rãi trong thực tế. Ví dụ, phương trình bậc hai có thể được sử dụng để tính toán quỹ đạo của vật thể, thiết kế các công trình xây dựng, và phân tích các hiện tượng kinh tế.
Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong sách giáo khoa, sách bài tập, và các đề thi thử. giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp bạn tự tin hơn trong các kỳ thi.
| Công thức | Mô tả |
|---|---|
| Δ = b2 - 4ac | Tính delta để xác định số nghiệm của phương trình bậc hai |
| x1,2 = (-b ± √Δ) / 2a | Tính nghiệm của phương trình bậc hai |
Hy vọng với những giải đáp chi tiết và hướng dẫn hữu ích trên đây, bạn sẽ tự tin hơn trong việc giải các câu hỏi trắc nghiệm trang 97, 98 Vở thực hành Toán 9. Chúc bạn học tập tốt!