Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các câu hỏi trắc nghiệm trang 103 Vở thực hành Toán 9 tập 2.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong môn Toán.
Khẳng định nào dưới đây là không đúng? A. Đa giác đều có các cạnh bằng nhau. B. Đa giác có các cạnh bằng nhau là đa giác đều. C. Đa giác đều có các góc bằng nhau. D. Đa giác đều nội tiếp được một đường tròn.
Trả lời Câu 1 trang 103 Vở thực hành Toán 9
Khẳng định nào dưới đây là không đúng?
A. Đa giác đều có các cạnh bằng nhau.
B. Đa giác có các cạnh bằng nhau là đa giác đều.
C. Đa giác đều có các góc bằng nhau.
D. Đa giác đều nội tiếp được một đường tròn.
Phương pháp giải:
+ Đa giác đều có tất cả các cạnh bằng nhau, tất cả các góc bằng nhau.
+ Đa giác đều nội tiếp được một đường tròn.
+ Đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau là đa giác đều.
Lời giải chi tiết:
+ Đa giác đều có tất cả các cạnh bằng nhau, tất cả các góc bằng nhau nên A, C đúng.
+ Đa giác đều nội tiếp được một đường tròn nên D đúng.
+ Đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau là đa giác đều nên B sai.
Chọn B
Trả lời Câu 3 trang 103 Vở thực hành Toán 9
Cho tam giác đều ABC với trọng tâm G. Phép quay nào dưới đây giữ nguyên tam giác ABC?
A. Phép quay thuận chiều \({60^o}\) tâm G.
B. Phép quay thuận chiều \({60^o}\) tâm A.
C. Phép quay thuận chiều \({120^o}\) tâm B.
D. Phép quay thuận chiều \({120^o}\) tâm G.
Phương pháp giải:
Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
Lời giải chi tiết:
Phép quay thuận chiều \({120^o}\) tâm G giữ nguyên tam giác ABC.
Chọn D
Trả lời Câu 2 trang 103 Vở thực hành Toán 9
Một đa giác đều có cạnh bằng a nội tiếp một đường tròn có bán kính bằng a. Chu vi của đa giác đó bằng
A. 3a.
B. 4a.
C. 6a.
D. 8a.
Phương pháp giải:
3 đường chéo chính của hình lục giác đều chia lục giác đều thành 6 tam giác đều bằng nhau. Từ đó, ta đi tính chu vi lục giác đều có cạnh bằng a.
Lời giải chi tiết:
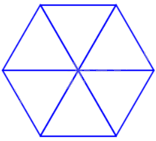
Hình lục giác đều cạnh a chia được thành 6 tam giác đều có độ dài mỗi cạnh bằng a (như hình vẽ).
Do đó, chu vi đa giác đó bằng 6a.
Chọn C
Chọn phương án trả lời đúng trong mỗi câu sau:
Trả lời Câu 1 trang 103 Vở thực hành Toán 9
Khẳng định nào dưới đây là không đúng?
A. Đa giác đều có các cạnh bằng nhau.
B. Đa giác có các cạnh bằng nhau là đa giác đều.
C. Đa giác đều có các góc bằng nhau.
D. Đa giác đều nội tiếp được một đường tròn.
Phương pháp giải:
+ Đa giác đều có tất cả các cạnh bằng nhau, tất cả các góc bằng nhau.
+ Đa giác đều nội tiếp được một đường tròn.
+ Đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau là đa giác đều.
Lời giải chi tiết:
+ Đa giác đều có tất cả các cạnh bằng nhau, tất cả các góc bằng nhau nên A, C đúng.
+ Đa giác đều nội tiếp được một đường tròn nên D đúng.
+ Đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau là đa giác đều nên B sai.
Chọn B
Trả lời Câu 2 trang 103 Vở thực hành Toán 9
Một đa giác đều có cạnh bằng a nội tiếp một đường tròn có bán kính bằng a. Chu vi của đa giác đó bằng
A. 3a.
B. 4a.
C. 6a.
D. 8a.
Phương pháp giải:
3 đường chéo chính của hình lục giác đều chia lục giác đều thành 6 tam giác đều bằng nhau. Từ đó, ta đi tính chu vi lục giác đều có cạnh bằng a.
Lời giải chi tiết:
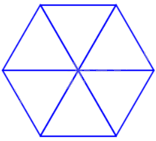
Hình lục giác đều cạnh a chia được thành 6 tam giác đều có độ dài mỗi cạnh bằng a (như hình vẽ).
Do đó, chu vi đa giác đó bằng 6a.
Chọn C
Trả lời Câu 3 trang 103 Vở thực hành Toán 9
Cho tam giác đều ABC với trọng tâm G. Phép quay nào dưới đây giữ nguyên tam giác ABC?
A. Phép quay thuận chiều \({60^o}\) tâm G.
B. Phép quay thuận chiều \({60^o}\) tâm A.
C. Phép quay thuận chiều \({120^o}\) tâm B.
D. Phép quay thuận chiều \({120^o}\) tâm G.
Phương pháp giải:
Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
Lời giải chi tiết:
Phép quay thuận chiều \({120^o}\) tâm G giữ nguyên tam giác ABC.
Chọn D
Trang 103 Vở thực hành Toán 9 tập 2 thường chứa các bài tập trắc nghiệm liên quan đến các chủ đề đã học trong chương. Các dạng bài tập thường gặp bao gồm: xác định hệ số của đa thức, tìm nghiệm của phương trình bậc hai, giải bài toán về hàm số bậc hai, và các bài tập ứng dụng thực tế.
Để giúp các em hiểu rõ hơn về nội dung và phương pháp giải các câu hỏi trắc nghiệm trang 103, chúng ta sẽ đi vào phân tích từng câu hỏi cụ thể.
Cho đa thức P(x) = 2x2 - 5x + 3. Hệ số của x2 là?
Lời giải: Hệ số của x2 trong đa thức P(x) = 2x2 - 5x + 3 là 2. Vậy đáp án đúng là C.
Phương trình x2 - 4x + 4 = 0 có nghiệm là?
Lời giải: Phương trình x2 - 4x + 4 = 0 có thể viết lại thành (x - 2)2 = 0. Do đó, x = 2 là nghiệm duy nhất của phương trình. Vậy đáp án đúng là A.
Để giải các bài tập trắc nghiệm trang 103 Vở thực hành Toán 9 tập 2 một cách hiệu quả, các em cần nắm vững các kiến thức sau:
Để tiết kiệm thời gian làm bài, các em có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em nên luyện tập thêm các bài tập tương tự trong sách giáo khoa, sách bài tập, và các đề thi thử.
Hy vọng với lời giải chi tiết và các phương pháp giải bài tập được trình bày ở trên, các em sẽ tự tin hơn khi giải các câu hỏi trắc nghiệm trang 103 Vở thực hành Toán 9 tập 2. Chúc các em học tập tốt!
| Chủ đề | Mức độ khó |
|---|---|
| Đa thức | Dễ |
| Phương trình bậc hai | Trung bình |
| Hàm số bậc hai | Khó |