Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 88 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) như hình bên. a) Biết rằng (widehat {AOC} = {60^o},widehat {BOD} = {80^o}). Tính số đo của góc AID. b) Chứng minh rằng (IA.IB = IC.ID).
Đề bài
Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) như hình bên.
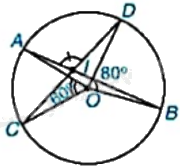
a) Biết rằng \(\widehat {AOC} = {60^o},\widehat {BOD} = {80^o}\). Tính số đo của góc AID.
b) Chứng minh rằng \(IA.IB = IC.ID\).
Phương pháp giải - Xem chi tiết
a) - Góc nội tiếp ADC và góc ở tâm AOC cùng chắn cung nhỏ AC nên \(\widehat {ADC} = \frac{{\widehat {AOC}}}{2}\).
- Góc nội tiếp BAD và góc ở tâm BOD cùng chắn cung nhỏ DB nên \(\widehat {BAD} = \frac{{\widehat {BOD}}}{2}\).
Do tổng ba góc trong tam giác AID bằng \({180^o}\) nên: \(\widehat {AID} = {180^o} - \widehat {IAD} - \widehat {IDA} = {180^o} - \widehat {ADC} - \widehat {BAD}\).
b) Chứng minh $\Delta IAC\backsim \Delta IDB\left( g.g \right)$, suy ra \(\frac{{IA}}{{ID}} = \frac{{IC}}{{IB}}\), hay \(IA.IB = IC.ID\).
Lời giải chi tiết
a) Xét đường tròn (O), ta có:
- Góc nội tiếp ADC và góc ở tâm AOC cùng chắn cung AC nên \(\widehat {ADC} = \frac{{\widehat {AOC}}}{2} = {30^o}\).
- Góc nội tiếp BAD và góc ở tâm BOD cùng chắn cung DB nên \(\widehat {BAD} = \frac{{\widehat {BOD}}}{2} = {40^o}\).
Do tổng ba góc trong tam giác AID bằng \({180^o}\) nên:
\(\widehat {AID} = {180^o} - \widehat {IAD} - \widehat {IDA} = {180^o} - \widehat {ADC} - \widehat {BAD} = {110^o}\)
b) Hai tam giác IAC và tam giác IDB có: \(\widehat {AIC} = \widehat {DIB}\) (hai góc đối đỉnh), \(\widehat {CAI} = \widehat {CAB} = \widehat {CDB} = \widehat {IDB}\) (vì \(\widehat {CAB}\) và \(\widehat {CDB}\) là hai góc nội tiếp của (O) cùng chắn cung nhỏ $\overset\frown{CB}$)
Suy ra $\Delta IAC\backsim \Delta IDB\left( g.g \right)$. Do đó, \(\frac{{IA}}{{ID}} = \frac{{IC}}{{IB}}\), hay \(IA.IB = IC.ID\).
Bài 4 trang 88 Vở thực hành Toán 9 tập 2 thường xoay quanh các chủ đề về hàm số bậc nhất, hệ số góc, và ứng dụng của hàm số trong việc giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số, đặc biệt là cách xác định hệ số góc và phương trình đường thẳng.
Trước khi bắt đầu giải bài, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài toán sẽ yêu cầu tìm phương trình đường thẳng, xác định hệ số góc, hoặc giải các bài toán liên quan đến ứng dụng của hàm số. Phương pháp giải thường bao gồm:
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài 4 trang 88. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một ví dụ minh họa:
Đề bài: Tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 6).
Lời giải:
Ngoài bài 4 trang 88, Vở thực hành Toán 9 tập 2 còn có nhiều bài tập tương tự về hàm số bậc nhất. Dưới đây là một số dạng bài tập thường gặp và cách giải:
Để học tốt môn Toán 9, đặc biệt là các bài tập về hàm số, bạn nên:
Bài 4 trang 88 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Bằng cách nắm vững các khái niệm cơ bản, luyện tập thường xuyên, và sử dụng các công cụ hỗ trợ, các em có thể tự tin giải quyết bài toán này và đạt kết quả tốt trong môn Toán 9.