Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 7 trang 100, 101 Vở thực hành Toán 9 tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, đầy đủ và kèm theo các giải thích chi tiết để bạn có thể nắm vững kiến thức.
Cho hình vuông ABCD nội tiếp (O) với (AB = 4cm). Hãy tính diện tích hình viên phân giới hạn bởi dây cung AB và cung nhỏ AB của (O).
Đề bài
Cho hình vuông ABCD nội tiếp (O) với \(AB = 4cm\). Hãy tính diện tích hình viên phân giới hạn bởi dây cung AB và cung nhỏ AB của (O).
Phương pháp giải - Xem chi tiết
Theo định lí Pythagore tính được AC, từ đó tính được bán kính R của (O).
+ Hình tròn tâm O bán kính R có diện tích là \({S_1} = \pi {R^2}\).
+ Hình vuông ABCD có diện tích là \({S_2} = A{B^2}\).
+ Vì bốn cạnh AB, BC, CD, DA của hình vuông lần lượt cùng với bốn cung nhỏ AB, BC, CD, DA giới hạn bốn hình viên phân bằng nhau nên mỗi hình này có diện tích là \(S = \frac{1}{4}\left( {{S_1} - {S_2}} \right)\)
Lời giải chi tiết
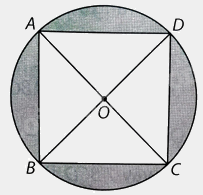
Theo định lí Pythagore, ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {16 + 16} = 4\sqrt 2 \left( {cm} \right)\).
Vậy đường tròn (O) có bán kính:
\(R = \frac{{AC}}{2} = 2\sqrt 2 \left( {cm} \right)\).
Hình tròn tâm O bán kính R có diện tích là \({S_1} = \pi {R^2} = 8\pi \left( {c{m^2}} \right)\).
Hình vuông ABCD có diện tích là \({S_2} = A{B^2} = 16\left( {c{m^2}} \right)\).
Vì bốn cạnh AB, BC, CD, DA của hình vuông lần lượt cùng với bốn cung nhỏ AB, BC, CD, DA giới hạn bốn hình viên phân bằng nhau nên mỗi hình này có diện tích là:
\(S = \frac{1}{4}\left( {{S_1} - {S_2}} \right) = \left( {2\pi - 4} \right)\left( {c{m^2}} \right)\).
Bài 7 trong Vở thực hành Toán 9 tập 2 tập trung vào việc giải phương trình bậc hai một ẩn. Đây là một phần kiến thức quan trọng trong chương trình Toán 9, giúp học sinh rèn luyện kỹ năng giải toán và áp dụng vào các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các công thức và phương pháp giải phương trình bậc hai đã được học.
Bài 7 bao gồm các dạng bài tập sau:
Lời giải:
Phương trình 2x2 - 5x + 2 = 0 có dạng ax2 + bx + c = 0 với a = 2, b = -5, c = 2.
Tính delta (Δ): Δ = b2 - 4ac = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (-b + √Δ) / 2a = (5 + √9) / (2 * 2) = (5 + 3) / 4 = 2
x2 = (-b - √Δ) / 2a = (5 - √9) / (2 * 2) = (5 - 3) / 4 = 0.5
Vậy, phương trình có hai nghiệm là x1 = 2 và x2 = 0.5
Lời giải:
Phương trình x2 - 4x + 4 = 0 có dạng ax2 + bx + c = 0 với a = 1, b = -4, c = 4.
Tính delta (Δ): Δ = b2 - 4ac = (-4)2 - 4 * 1 * 4 = 16 - 16 = 0
Vì Δ = 0, phương trình có nghiệm kép:
x = -b / 2a = -(-4) / (2 * 1) = 4 / 2 = 2
Vậy, phương trình có nghiệm kép là x = 2
Lời giải:
Phương trình x2 - 3x + 2 = 0 có thể được phân tích thành nhân tử:
(x - 1)(x - 2) = 0
Suy ra, x - 1 = 0 hoặc x - 2 = 0
Vậy, phương trình có hai nghiệm là x1 = 1 và x2 = 2
Để giải nhanh phương trình bậc hai, bạn có thể sử dụng một số mẹo sau:
Để nắm vững kiến thức về phương trình bậc hai, bạn nên luyện tập thêm các bài tập khác trong Vở thực hành Toán 9 tập 2 và các tài liệu tham khảo khác. Hãy tìm kiếm các bài tập có mức độ khó tăng dần để rèn luyện kỹ năng giải toán của mình.
Bài 7 trang 100, 101 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về phương trình bậc hai. Hy vọng rằng với lời giải chi tiết và các mẹo giải nhanh được cung cấp trong bài viết này, bạn sẽ có thể giải quyết bài toán một cách dễ dàng và hiệu quả. Chúc bạn học tốt!