Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 65, 66 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Cho biểu đồ sau: a) Lập bảng tần số tương đối cho dữ liệu được biểu diễn trên biểu đồ. b) Giả sử để có kết quả trên PISA đã khảo sát trên 10 000 trẻ em 15 tuổi tại Việt Nam. Lập bảng tần số biểu diễn số lượng trẻ theo các mức đọc thành thạo.
Đề bài
Cho biểu đồ sau:
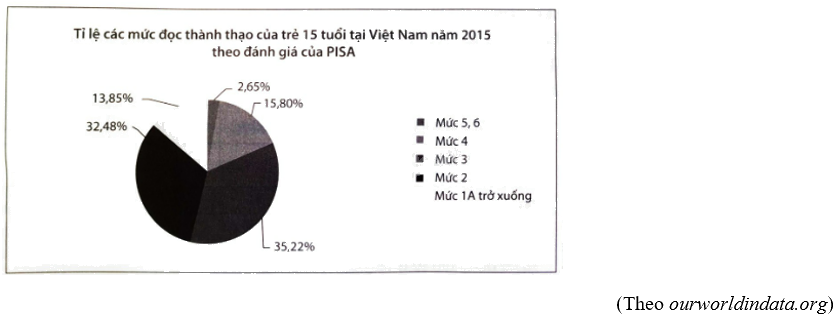
a) Lập bảng tần số tương đối cho dữ liệu được biểu diễn trên biểu đồ.
b) Giả sử để có kết quả trên PISA đã khảo sát trên 10 000 trẻ em 15 tuổi tại Việt Nam. Lập bảng tần số biểu diễn số lượng trẻ theo các mức đọc thành thạo.
Phương pháp giải - Xem chi tiết
a) + Chỉ ra tần số tương đối của từng nhóm số liệu đã có trong biểu đồ.
+ Lập bảng tần số tương đối có dạng:
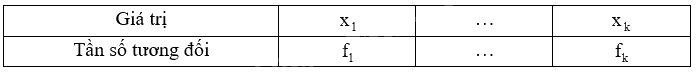
b) + Tính tần số của từng giá trị trong biểu đồ.
+ Lập bảng tần số có dạng như sau:
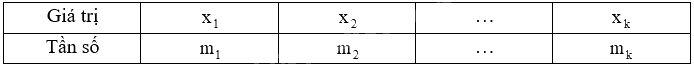
Trong bảng tần số, ta chỉ liệt kê các giá trị \({x_i}\) khác nhau, các giá trị \({x_i}\) này có thể không là số.
Lời giải chi tiết
a) Bảng tần số tương đối:

b) Số trẻ em theo các mức độ đọc thành thạo lần lượt là:
Mức 1A trở xuống: \(10\;000.13,85\% = 1385\) (em)
Mức 2: \(10\;000.32,48\% = 3248\) (em)
Mức 3: \(10\;000.35,22\% = 3522\) (em)
Mức 4: \(10\;000.15,80\% = 1580\) (em)
Mức 5, 6: \(10\;000.2,65\% = 265\) (em)
Ta có bảng tần số sau:

Bài 4 trang 65, 66 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình ôn tập về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng áp dụng công thức.
Bài 4 bao gồm các dạng bài tập sau:
Để xác định hệ số góc và tung độ gốc của hàm số bậc nhất có dạng y = ax + b, ta cần phân tích phương trình và xác định giá trị của a và b. Hệ số a được gọi là hệ số góc, cho biết độ dốc của đường thẳng. Tung độ gốc b là giá trị của y khi x = 0, tức là tọa độ giao điểm của đường thẳng với trục Oy.
Ví dụ: Cho hàm số y = 2x - 3. Hệ số góc a = 2, tung độ gốc b = -3.
Để vẽ đồ thị hàm số bậc nhất, ta thực hiện các bước sau:
Ví dụ: Vẽ đồ thị hàm số y = x + 1. Ta chọn hai điểm A(0, 1) và B(1, 2). Vẽ đường thẳng đi qua hai điểm A và B, ta được đồ thị hàm số y = x + 1.
Để tìm tọa độ giao điểm của hai đường thẳng, ta giải hệ phương trình bậc nhất hai ẩn, trong đó mỗi phương trình đại diện cho một đường thẳng. Nghiệm của hệ phương trình là tọa độ giao điểm của hai đường thẳng.
Ví dụ: Tìm tọa độ giao điểm của hai đường thẳng y = 2x + 1 và y = -x + 4. Ta giải hệ phương trình:
| y = 2x + 1 | y = -x + 4 |
Thay y = 2x + 1 vào phương trình y = -x + 4, ta được: 2x + 1 = -x + 4. Giải phương trình này, ta được x = 1. Thay x = 1 vào phương trình y = 2x + 1, ta được y = 3. Vậy tọa độ giao điểm của hai đường thẳng là (1, 3).
Các bài toán ứng dụng hàm số bậc nhất thường liên quan đến các tình huống thực tế, như tính quãng đường, thời gian, chi phí,... Để giải các bài toán này, ta cần xác định được hàm số bậc nhất mô tả mối quan hệ giữa các đại lượng và sử dụng các kiến thức đã học để giải quyết bài toán.
Bài 4 trang 65, 66 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết bài tập một cách hiệu quả. Chúc các em học tập tốt!