Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 5 trang 100 Vở thực hành Toán 9 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho tam giác ABC cân tại A có ba đỉnh nằm trên đường tròn (O). Đường cao AH cắt (O) tại D. Biết (BC = 24cm,AC = 20cm). Tính chiều cao AH và bán kính đường tròn (O).
Đề bài
Cho tam giác ABC cân tại A có ba đỉnh nằm trên đường tròn (O). Đường cao AH cắt (O) tại D. Biết \(BC = 24cm,AC = 20cm\). Tính chiều cao AH và bán kính đường tròn (O).
Phương pháp giải - Xem chi tiết
+ Chứng minh H là trung điểm của BC nên tính được HC.
+ Tam giác ACH vuông tại H nên theo định lí Pythagore, ta tính được AH.
+ Chứng minh tam giác ACD vuông tại C.
+ Trong tam giác ACD vuông tại C ta có: \(A{C^2} = AH.AD\) nên tính được AD
+ Bán kính của đường tròn (O) là \(R = \frac{{AD}}{2}\).
Lời giải chi tiết
(H.5.5)
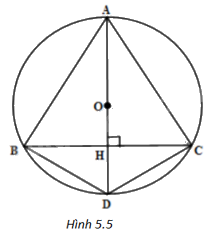
Vì tam giác ABC cân tại A nên đường cao AH cũng là đường trung trực của đoạn BC, suy ra H là trung điểm của BC.
Tam giác ACH vuông tại H nên theo định lí Pythagore, ta được \(A{H^2} = A{C^2} - H{C^2}\), suy ra \(AH = 16cm\).
Tam giác ACD có AD là đường kính của đường tròn (O) nên tam giác ACD vuông tại C.
Trong tam giác ACD vuông tại C ta có: \(A{C^2} = AH.AD\), suy ra \(AD = \frac{{A{C^2}}}{{AH}} = 25cm\).
Vậy bán kính của đường tròn (O) là \(R = \frac{{AD}}{2} = \frac{{25}}{2}cm\).
Bài 5 trang 100 Vở thực hành Toán 9 thường thuộc các chủ đề về hàm số bậc nhất, hệ số góc, đường thẳng song song và vuông góc. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về hàm số, cách xác định hệ số góc và điều kiện để hai đường thẳng song song hoặc vuông góc.
Trước khi bắt đầu giải bài tập, hãy đọc kỹ đề bài và xác định rõ yêu cầu. Thông thường, bài tập sẽ yêu cầu tìm phương trình đường thẳng, xác định hệ số góc hoặc chứng minh một tính chất nào đó. Dựa vào yêu cầu của đề bài, ta có thể áp dụng các phương pháp giải sau:
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 5 trang 100 Vở thực hành Toán 9. Giả sử bài tập yêu cầu tìm phương trình đường thẳng đi qua hai điểm A(x1, y1) và B(x2, y2). Lời giải sẽ như sau:
k = (y2 - y1) / (x2 - x1)
y - y1 = k(x - x1)
Cho hai điểm A(1, 2) và B(3, 4). Hãy tìm phương trình đường thẳng AB.
Giải:
Ngoài bài tập tìm phương trình đường thẳng, bài 5 trang 100 Vở thực hành Toán 9 còn có thể xuất hiện các dạng bài tập khác như:
Để giải các dạng bài tập này, bạn cần nắm vững các khái niệm và công thức liên quan đến hàm số bậc nhất và đường thẳng.
Bài 5 trang 100 Vở thực hành Toán 9 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và đường thẳng. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ tự tin hơn khi giải bài tập này. Chúc bạn học tập tốt!
| Công thức | Mô tả |
|---|---|
| y = ax + b | Phương trình hàm số bậc nhất |
| a | Hệ số góc |
| b | Tung độ gốc |