Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 58, 59 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Người ta trồng cà rốt và thử nghiệm một loại phân bón mới. Khi thu hoạch người ta đo chiều dài các của cà rốt thu được kết quả sau: Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng thống kê trên.
Đề bài
Người ta trồng cà rốt và thử nghiệm một loại phân bón mới. Khi thu hoạch người ta đo chiều dài các của cà rốt thu được kết quả sau:

Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng thống kê trên.
Phương pháp giải - Xem chi tiết
+ Lập bảng tần số tương đối ghép nhóm.
+ Cách vẽ biểu đồ tần số tương đối ghép nhóm dạng cột:
Bước 1: Vẽ trục đứng, trục ngang. Trên trục đứng xác định đơn vị độ dài phù hợp với các tần số tương đối. Trên trục ngang xác định các nhóm số liệu cần biểu diễn.
Bước 2: Dựng các hình cột (kề nhau) ứng với các nhóm dữ liệu, mỗi hình chột có chiều cao bằng tần số tương đối của nhóm số liệu.
Bước 3: Ghi chú giải cho các trục, các cột và tiêu đề cho biểu đồ.
Lời giải chi tiết
Tổng số củ cà rốt là: \(8 + 17 + 30 + 28 + 12 + 5 = 100\)
Tần số tương đối tương ứng với các nhóm lần lượt là: \(\frac{8}{{100}}.100\% = 8\% ;\frac{{17}}{{100}} = 17\% ;\frac{{30}}{{100}}.100\% = 30\% ;\frac{{28}}{{100}}.100\% = 28\% ;\frac{{12}}{{100}}.100\% = 12\% ;\frac{5}{{100}}.100\% = 5\% \).
Ta có bảng tần số tương đối ghép nhóm:

Biểu đồ tần số tương đối ghép nhóm dạng cột:
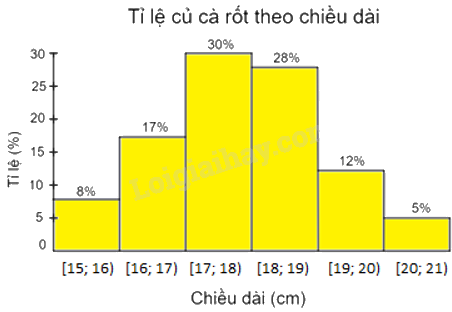
Bài 4 trang 58, 59 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình ôn tập về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giải bài 4 trang 58, 59 Vở thực hành Toán 9 tập 2 một cách hiệu quả, các em cần nắm vững các kiến thức sau:
Ví dụ minh họa:
Cho hàm số y = 2x - 1. Hãy xác định hệ số a và vẽ đồ thị của hàm số.
Giải:
Hệ số a của hàm số là 2. Vì a > 0 nên hàm số đồng biến.
Để vẽ đồ thị, ta xác định hai điểm thuộc đường thẳng:
Vẽ đường thẳng đi qua hai điểm A(0; -1) và B(1; 1), ta được đồ thị của hàm số y = 2x - 1.
Để củng cố kiến thức về hàm số bậc nhất, các em có thể luyện tập thêm các bài tập sau:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em sẽ hiểu rõ hơn về hàm số bậc nhất và tự tin giải quyết các bài tập tương tự. Chúc các em học tập tốt!
Ngoài các dạng bài tập đã nêu trên, bài 4 trang 58, 59 Vở thực hành Toán 9 tập 2 còn có thể xuất hiện các dạng bài tập khác như:
Để giải các dạng bài tập này, các em cần vận dụng các kiến thức về phương trình bậc nhất một ẩn và hệ phương trình bậc nhất hai ẩn.
Các em có thể tham khảo thêm các tài liệu sau để hiểu rõ hơn về hàm số bậc nhất:
Hy vọng những thông tin trên sẽ giúp các em học tập tốt môn Toán 9.