Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 87 Vở thực hành Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, hỗ trợ các em học Toán 9 một cách hiệu quả và thú vị.
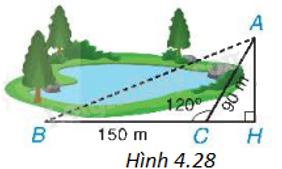
Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là (CA = 90m,CB = 150m) và (widehat {ACB} = {120^o}) (H.4.28). Hãy tính AB giúp bạn.
Đề bài
Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là \(CA = 90m,CB = 150m\) và \(\widehat {ACB} = {120^o}\) (H.4.28). Hãy tính AB giúp bạn.
Phương pháp giải - Xem chi tiết
+ Kẻ đường cao AH của tam giác ABC thì C nằm giữa B và H.
+ \(\widehat {ACH} = {180^o} - \widehat {ACB} = {60^o}\)
+ Trong tam giác ACH vuông tại H nên \(HC = AC.\cos \widehat {ACH}\), tính được HC, \(AH = AC.\sin \widehat {ACH}\) tính được AH.
+ \(BH = BC + CH\)
+ Áp dụng định lí Pythagore vào tam giác ABH vuông tại H, tính được AB.
Lời giải chi tiết
Kẻ đường cao AH của tam giác ABC thì C nằm giữa B và H.
Trong tam giác ACH, ta có \(\widehat {ACH} = {180^o} - \widehat {ACB} = {60^o}\),
\(HC = AC.\cos \widehat {ACH} = 90.\cos {60^o} = 45\left( m \right)\)
\(AH = AC.\sin \widehat {ACH} = 90.\sin {60^o} = 45\sqrt 3 \left( m \right)\)
Từ đó, \(BH = BC + CH = 150 + 45 = 195\left( m \right)\)
\(A{B^2} = B{H^2} + A{H^2} = {195^2} + {\left( {45\sqrt 3 } \right)^2}\) suy ra \(AB = 210\left( m \right)\)
Bài 5 trang 87 Vở thực hành Toán 9 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 5 trang 87 Vở thực hành Toán 9 thường bao gồm các dạng bài tập sau:
Để giải bài 5 trang 87 Vở thực hành Toán 9 một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:
Bài tập: Cho hàm số y = 2x - 1. Tìm tọa độ giao điểm của đường thẳng này với đường thẳng y = -x + 2.
Giải:
Để tìm tọa độ giao điểm, ta giải hệ phương trình:
| y = 2x - 1 | y = -x + 2 |
Thay y = 2x - 1 vào phương trình y = -x + 2, ta được:
2x - 1 = -x + 2
3x = 3
x = 1
Thay x = 1 vào phương trình y = 2x - 1, ta được:
y = 2(1) - 1 = 1
Vậy tọa độ giao điểm của hai đường thẳng là (1; 1).
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong Vở thực hành Toán 9 và các tài liệu học tập khác. Ngoài ra, các em cũng có thể tìm kiếm các bài giảng online hoặc tham gia các khóa học Toán 9 để được hướng dẫn chi tiết hơn.
Học Toán 9 đòi hỏi sự kiên trì, chăm chỉ và phương pháp học tập đúng đắn. Các em nên dành thời gian ôn tập bài cũ, làm bài tập đầy đủ và tìm kiếm sự giúp đỡ của giáo viên hoặc bạn bè khi gặp khó khăn. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!