Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 72, 73 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất và ứng dụng của nó trong giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Có hai túi A và B. Túi A đựng ba tấm thẻ ghi các số 5, 6, 7. Túi B đựng 4 tấm thẻ ghi các số 1, 2, 3, 4. Rút ngẫu nhiên từ mỗi túi một tấm thẻ. a) Phép thử và kết quả của phép thử là gì? b) Mô tả không gian mẫu của phép thử. Không gian mẫu có bao nhiêu phần tử?
Đề bài
Có hai túi A và B. Túi A đựng ba tấm thẻ ghi các số 5, 6, 7. Túi B đựng 4 tấm thẻ ghi các số 1, 2, 3, 4. Rút ngẫu nhiên từ mỗi túi một tấm thẻ.
a) Phép thử và kết quả của phép thử là gì?
b) Mô tả không gian mẫu của phép thử. Không gian mẫu có bao nhiêu phần tử?
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về phép thử để tìm phép thử: Một hoặc một số hành động, thực nghiệm được tiến hành liên tiếp hay đồng thời mà kết quả của chúng không thể biết được trước khi thực hiện nhưng có thể liệt kê các kết quả có thể xảy ra, được gọi là một phép thử ngẫu nhiên, gọi tắt là phép thử.
b) Sử dụng kiến thức về không gian mẫu để tìm không gian mẫu: Sử dụng kiến thức về không gian mẫu để tìm không gian mẫu: Tập hợp tất cả các kết quả có thể xảy ra của phép thử (gọi tắt là tập tất cả các kết quả có thể của phép thử) được gọi là không gian mẫu của phép thử.
Lời giải chi tiết
a) Phép thử là rút ngẫu nhiên từ mỗi túi một tấm thẻ.
Kết quả của phép thử là cặp số (a, b) trong đó a và b lần lượt là số ghi trên tấm thẻ rút ra ở túi A và B.
b) Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng:
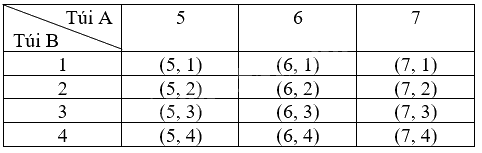
Mỗi ô trong bảng là một kết quả có thể. Không gian mẫu là $\Omega = $ {(5, 1); (5, 2); (5, 3); (5, 4); (6, 1); (6, 2); (6, 3); (6, 4); (7, 1); (7, 2); (7, 3); (7, 4)}.
Vậy không gian mẫu có 12 phần tử.
Bài 6 trong Vở thực hành Toán 9 tập 2 tập trung vào việc vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán liên quan đến đường thẳng và ứng dụng thực tế. Các bài tập thường yêu cầu học sinh xác định hệ số góc, phương trình đường thẳng, và giải các bài toán có tính ứng dụng cao.
Bài 6 bao gồm các dạng bài tập sau:
Đề bài: (Ví dụ: Cho đường thẳng y = 2x + 1. Xác định hệ số góc của đường thẳng này.)
Giải: Hệ số góc của đường thẳng y = 2x + 1 là 2.
Đề bài: (Ví dụ: Viết phương trình đường thẳng đi qua điểm A(1; 2) và có hệ số góc là -1.)
Giải: Phương trình đường thẳng có dạng y = -x + b. Thay tọa độ điểm A(1; 2) vào phương trình, ta có: 2 = -1 + b => b = 3. Vậy phương trình đường thẳng là y = -x + 3.
Đề bài: (Ví dụ: Một ô tô đi từ A đến B với vận tốc 60km/h. Hãy viết hàm số biểu thị quãng đường đi được của ô tô theo thời gian.)
Giải: Gọi s là quãng đường đi được (km) và t là thời gian đi (giờ). Hàm số biểu thị quãng đường đi được của ô tô theo thời gian là s = 60t.
Ngoài Vở thực hành Toán 9 tập 2, các em có thể tham khảo thêm:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ hiểu rõ hơn về bài 6 trang 72, 73 Vở thực hành Toán 9 tập 2 và có thể tự tin giải các bài tập tương tự. Chúc các em học tập tốt!