Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trắc nghiệm trong Vở thực hành Toán 9. Chúng tôi hiểu rằng việc giải các bài tập này có thể gặp nhiều khó khăn, đặc biệt là đối với những học sinh mới bắt đầu làm quen với phương pháp trắc nghiệm.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi đã biên soạn bộ giải đáp đầy đủ, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho đường thẳng a và một điểm O cách a một khoảng bằng 6cm. Khẳng định nào sau đây là đúng về vị trí tương đối của đường thẳng a và đường tròn (O; 9cm)? A. Đường thẳng a cắt đường tròn (O) tại hai điểm. B. Đường thẳng a tiếp xúc với đường tròn (O). C. Đường thẳng a và đường tròn (O) không có điểm chung. D. Đường thẳng a và đường tròn (O) có duy nhất điểm chung.
Trả lời Câu 1 trang 112 Vở thực hành Toán 9
Cho đường thẳng a và một điểm O cách a một khoảng bằng 6cm. Khẳng định nào sau đây là đúng về vị trí tương đối của đường thẳng a và đường tròn (O; 9cm)?
A. Đường thẳng a cắt đường tròn (O) tại hai điểm.
B. Đường thẳng a tiếp xúc với đường tròn (O).
C. Đường thẳng a và đường tròn (O) không có điểm chung.
D. Đường thẳng a và đường tròn (O) có duy nhất điểm chung.
Phương pháp giải:
Cho đường thẳng a và đường tròn (O; R). Gọi d là khoảng cách từ O đến a. Khi đó:
+ Đường thẳng a và đường tròn (O; R) cắt nhau khi \(d < R\).
+ Đường thẳng a và đường tròn (O; R) tiếp xúc với nhau khi \(d = R\).
+ Đường thẳng a và đường tròn (O; R) không giao nhau khi \(d > R\).
Lời giải chi tiết:
Vì \(6cm < 9cm\) nên đường thẳng a cắt đường tròn (O) tại hai điểm.
Chọn A
Trả lời Câu 4 trang 113 Vở thực hành Toán 9
Cho đường tròn (O) và điểm M nằm ngoài đường tròn, vẽ hai tiếp tuyến MA và MB của đường tròn (O). Biết \(\widehat {AMB} = {35^o}\). Số đo cung nhỏ AB là
A. \({145^o}\).
B. \({215^o}\).
C. \({125^o}\).
D. \({235^o}\).
Phương pháp giải:
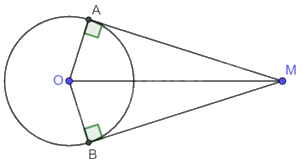
+ Chứng minh \(\widehat {MAO} = \widehat {MBO} = {90^o}\).
+ Tứ giác \(\widehat {MAO} + \widehat {MBO} + \widehat {AMB} + \widehat {AOB} = {360^o}\), từ đó tính được góc AOB, suy ra số đo cung nhỏ AB.
Lời giải chi tiết:
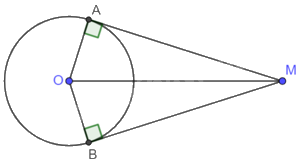
Vì MA, MB là tiếp tuyến của đường tròn (O) nên \(MA \bot OA,MB \bot OB\) nên \(\widehat {MAO} = \widehat {MBO} = {90^o}\).
Tứ giác MBOA có: \(\widehat {MAO} + \widehat {MBO} + \widehat {AMB} + \widehat {AOB} = {360^o}\)
\(\widehat {AOB} = {360^o} - \widehat {MAO} - \widehat {MBO} - \widehat {AMB} = {360^o} - {90^o} - {90^o} - {35^o} = {145^o}\)
Vì góc ở tâm AOB chắn cung nhỏ AB nên số đo cung nhỏ AB bằng \({145^o}\).
Chọn A
Trả lời Câu 3 trang 112 Vở thực hành Toán 9
Cho đường thẳng a và một điểm O cách a là 3cm. Vẽ đường tròn (O; 5cm). Gọi B, C là các giao điểm của đường thẳng a và (O). Diện tích của tam giác OBC bằng
A. \(10c{m^2}\).
B. \(6c{m^2}\).
C. \(24c{m^2}\).
D. \(12c{m^2}\).
Phương pháp giải:
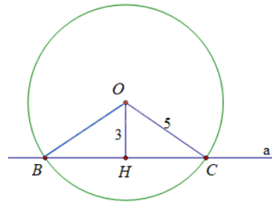
+ Qua O kẻ đường thẳng vuông góc với BC tại H. Khi đó, OH là khoảng cách từ O đến đường thẳng a. Do đó, \(OH = 3cm\).
+ Chứng minh tam giác OBC cân tại O, suy ra OH là đường trung tuyến, suy ra \(BH = HC = \frac{1}{2}BC\).
+ Áp dụng định lí Pythagore vào tam giác BOH vuông tại H tính được BH, từ đó tính được BC.
+ Diện tích tam giác OBC là: \(S = \frac{1}{2}OH.BC\)
Lời giải chi tiết:
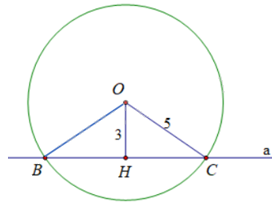
Qua O kẻ đường thẳng vuông góc với BC tại H. Khi đó, OH là khoảng cách từ O đến đường thẳng a. Do đó, \(OH = 3cm\).
Tam giác OBC có: \(OB = OC\) (bán kính (O)) nên tam giác BOC cân tại O. Do đó, OH là đường cao đồng thời là đường trung tuyến của tam giác OBC. Suy ra \(BH = HC = \frac{1}{2}BC\).
Áp dụng định lí Pythagore vào tam giác BOH vuông tại H có:
\(O{H^2} + B{H^2} = O{B^2}\) nên \(BH = \sqrt {B{O^2} - O{H^2}} = \sqrt {{5^2} - {3^2}} = 4\left( {cm} \right)\) nên \(BC = 2BH = 2.4 = 8\left( {cm} \right)\)
Diện tích tam giác OBC là: \(S = \frac{1}{2}OH.BC = \frac{1}{2}.3.8 = 12\left( {c{m^2}} \right)\)
Chọn D
Trả lời Câu 2 trang 112 Vở thực hành Toán 9
Cho một điểm M nằm ngoài đường tròn (I; 6cm), vẽ tiếp tuyến MB đến đường tròn đó (B là tiếp điểm). Nếu \(MI = 10cm\) thì độ dài MB bằng
A. 6 cm.
B. 8 cm.
C. 7 cm.
D. 10 cm.
Phương pháp giải:
+ Chứng minh tam giác MBI vuông tại B.
+ Áp dụng định lí Pythagore vào tam giác MBI vuông tại B ta tính được MB.
Lời giải chi tiết:
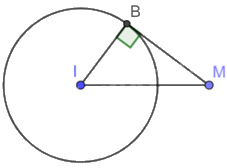
Vì MB là tiếp tuyến của (I) nên \(MB \bot IB\) tại B. Khi đó tam giác IMB vuông tại B.
Áp dụng định lí Pythagore vào tam giác MBI vuông tại B ta có:
\(I{B^2} + M{B^2} = M{I^2}\)
\(MB = \sqrt {M{I^2} - I{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\left( {cm} \right)\)
Chọn B
Chọn phương án đúng trong mỗi câu sau:
Trả lời Câu 1 trang 112 Vở thực hành Toán 9
Cho đường thẳng a và một điểm O cách a một khoảng bằng 6cm. Khẳng định nào sau đây là đúng về vị trí tương đối của đường thẳng a và đường tròn (O; 9cm)?
A. Đường thẳng a cắt đường tròn (O) tại hai điểm.
B. Đường thẳng a tiếp xúc với đường tròn (O).
C. Đường thẳng a và đường tròn (O) không có điểm chung.
D. Đường thẳng a và đường tròn (O) có duy nhất điểm chung.
Phương pháp giải:
Cho đường thẳng a và đường tròn (O; R). Gọi d là khoảng cách từ O đến a. Khi đó:
+ Đường thẳng a và đường tròn (O; R) cắt nhau khi \(d < R\).
+ Đường thẳng a và đường tròn (O; R) tiếp xúc với nhau khi \(d = R\).
+ Đường thẳng a và đường tròn (O; R) không giao nhau khi \(d > R\).
Lời giải chi tiết:
Vì \(6cm < 9cm\) nên đường thẳng a cắt đường tròn (O) tại hai điểm.
Chọn A
Trả lời Câu 2 trang 112 Vở thực hành Toán 9
Cho một điểm M nằm ngoài đường tròn (I; 6cm), vẽ tiếp tuyến MB đến đường tròn đó (B là tiếp điểm). Nếu \(MI = 10cm\) thì độ dài MB bằng
A. 6 cm.
B. 8 cm.
C. 7 cm.
D. 10 cm.
Phương pháp giải:
+ Chứng minh tam giác MBI vuông tại B.
+ Áp dụng định lí Pythagore vào tam giác MBI vuông tại B ta tính được MB.
Lời giải chi tiết:
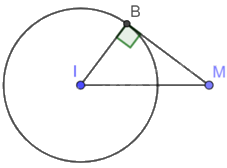
Vì MB là tiếp tuyến của (I) nên \(MB \bot IB\) tại B. Khi đó tam giác IMB vuông tại B.
Áp dụng định lí Pythagore vào tam giác MBI vuông tại B ta có:
\(I{B^2} + M{B^2} = M{I^2}\)
\(MB = \sqrt {M{I^2} - I{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\left( {cm} \right)\)
Chọn B
Trả lời Câu 3 trang 112 Vở thực hành Toán 9
Cho đường thẳng a và một điểm O cách a là 3cm. Vẽ đường tròn (O; 5cm). Gọi B, C là các giao điểm của đường thẳng a và (O). Diện tích của tam giác OBC bằng
A. \(10c{m^2}\).
B. \(6c{m^2}\).
C. \(24c{m^2}\).
D. \(12c{m^2}\).
Phương pháp giải:
+ Qua O kẻ đường thẳng vuông góc với BC tại H. Khi đó, OH là khoảng cách từ O đến đường thẳng a. Do đó, \(OH = 3cm\).
+ Chứng minh tam giác OBC cân tại O, suy ra OH là đường trung tuyến, suy ra \(BH = HC = \frac{1}{2}BC\).
+ Áp dụng định lí Pythagore vào tam giác BOH vuông tại H tính được BH, từ đó tính được BC.
+ Diện tích tam giác OBC là: \(S = \frac{1}{2}OH.BC\)
Lời giải chi tiết:
Qua O kẻ đường thẳng vuông góc với BC tại H. Khi đó, OH là khoảng cách từ O đến đường thẳng a. Do đó, \(OH = 3cm\).
Tam giác OBC có: \(OB = OC\) (bán kính (O)) nên tam giác BOC cân tại O. Do đó, OH là đường cao đồng thời là đường trung tuyến của tam giác OBC. Suy ra \(BH = HC = \frac{1}{2}BC\).
Áp dụng định lí Pythagore vào tam giác BOH vuông tại H có:
\(O{H^2} + B{H^2} = O{B^2}\) nên \(BH = \sqrt {B{O^2} - O{H^2}} = \sqrt {{5^2} - {3^2}} = 4\left( {cm} \right)\) nên \(BC = 2BH = 2.4 = 8\left( {cm} \right)\)
Diện tích tam giác OBC là: \(S = \frac{1}{2}OH.BC = \frac{1}{2}.3.8 = 12\left( {c{m^2}} \right)\)
Chọn D
Trả lời Câu 4 trang 113 Vở thực hành Toán 9
Cho đường tròn (O) và điểm M nằm ngoài đường tròn, vẽ hai tiếp tuyến MA và MB của đường tròn (O). Biết \(\widehat {AMB} = {35^o}\). Số đo cung nhỏ AB là
A. \({145^o}\).
B. \({215^o}\).
C. \({125^o}\).
D. \({235^o}\).
Phương pháp giải:
+ Chứng minh \(\widehat {MAO} = \widehat {MBO} = {90^o}\).
+ Tứ giác \(\widehat {MAO} + \widehat {MBO} + \widehat {AMB} + \widehat {AOB} = {360^o}\), từ đó tính được góc AOB, suy ra số đo cung nhỏ AB.
Lời giải chi tiết:
Vì MA, MB là tiếp tuyến của đường tròn (O) nên \(MA \bot OA,MB \bot OB\) nên \(\widehat {MAO} = \widehat {MBO} = {90^o}\).
Tứ giác MBOA có: \(\widehat {MAO} + \widehat {MBO} + \widehat {AMB} + \widehat {AOB} = {360^o}\)
\(\widehat {AOB} = {360^o} - \widehat {MAO} - \widehat {MBO} - \widehat {AMB} = {360^o} - {90^o} - {90^o} - {35^o} = {145^o}\)
Vì góc ở tâm AOB chắn cung nhỏ AB nên số đo cung nhỏ AB bằng \({145^o}\).
Chọn A
Trang 112 và 113 Vở thực hành Toán 9 thường chứa các bài tập trắc nghiệm liên quan đến các chủ đề quan trọng như hàm số bậc nhất, hệ phương trình bậc nhất hai ẩn, và các ứng dụng thực tế của đại số. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập trắc nghiệm là rất quan trọng để đạt kết quả tốt trong các kỳ thi.
Các bài tập trắc nghiệm trên trang 112 và 113 thường bao gồm các dạng sau:
Chúng ta sẽ đi vào giải chi tiết từng câu hỏi trắc nghiệm trên trang 112. (Ở đây sẽ là nội dung giải chi tiết từng câu hỏi, ví dụ):
Câu 1: (Nội dung câu hỏi)...
Giải: (Lời giải chi tiết, bao gồm các bước giải và giải thích rõ ràng)...
Đáp án: (Đáp án đúng)...
Tương tự như trang 112, chúng ta sẽ giải chi tiết từng câu hỏi trắc nghiệm trên trang 113. (Ở đây sẽ là nội dung giải chi tiết từng câu hỏi, ví dụ):
Câu 1: (Nội dung câu hỏi)...
Giải: (Lời giải chi tiết, bao gồm các bước giải và giải thích rõ ràng)...
Đáp án: (Đáp án đúng)...
Để giải bài tập trắc nghiệm Toán 9 hiệu quả, bạn có thể áp dụng một số mẹo sau:
Ngoài Vở thực hành Toán 9, bạn có thể tham khảo thêm các tài liệu sau để học Toán 9 hiệu quả:
Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải các câu hỏi trắc nghiệm trang 112, 113 Vở thực hành Toán 9. Chúc bạn học tập tốt!