Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 60, 61 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình đại số, tập trung vào việc giải các bài toán liên quan đến hàm số bậc nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Cho biểu đồ tần số ghép nhóm dạng cột: Lập bảng tần số và bảng tần số tương đối ghép nhóm cho dữ liệu được biểu diễn trên biểu đồ.
Đề bài
Cho biểu đồ tần số ghép nhóm dạng cột:
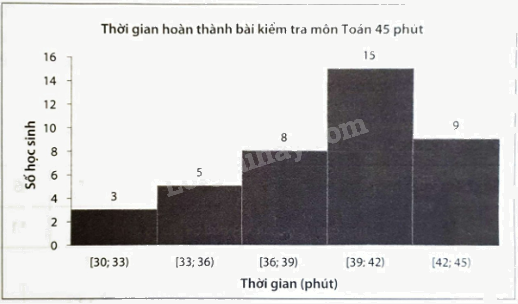
Lập bảng tần số và bảng tần số tương đối ghép nhóm cho dữ liệu được biểu diễn trên biểu đồ.
Phương pháp giải - Xem chi tiết
+ Lập bảng tần số ghép nhóm về thời gian hoàn thành bài kiểm tra môn Toán.
Cho bảng tần số:

Trong đó, tần số \({m_i}\) của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) là số giá trị của mẫu số liệu lớn hơn hoặc bằng \({a_i}\) và nhỏ hơn \({a_{i + 1}}\).
+ Lập bảng tần số tương đối ghép nhóm về thời gian hoàn thành bài kiểm tra môn Toán.
- Tính tần số tương đối ứng với các giá trị trong mẫu dữ liệu: Nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) có tần số \({m_i}\) thì có tần số tương đối là: \({f_i} = \frac{{{m_i}}}{n}.100\left( \% \right)\) với m là tổng tất cả các tần số có trong mẫu số liệu.
Bảng tần số tương đối ghép nhóm có dạng:

Lời giải chi tiết
Bảng tần số ghép nhóm:

Tổng số học sinh là: \(3 + 5 + 8 + 15 + 9 = 40\) (học sinh)
Tần số tương đối của các nhóm lần lượt là:
\(\frac{3}{{40}}.100\% = 7,5\% ;\frac{5}{{40}}.100\% = 12,5\% ;\frac{8}{{40}}.100\% = 20\% ;\frac{{15}}{{40}}.100\% = 37,5\% ;\frac{9}{{40}}.100\% = 22,5\% \)
Bảng tần số tương đối ghép nhóm:

Bài 7 trong Vở thực hành Toán 9 tập 2 tập trung vào việc củng cố kiến thức về hàm số bậc nhất, bao gồm việc xác định hệ số góc, đường thẳng song song và vuông góc. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và áp dụng linh hoạt các công thức đã học.
Trước khi đi vào giải bài tập, chúng ta cùng ôn lại một số kiến thức lý thuyết quan trọng:
Bài 7 thường bao gồm các dạng bài tập sau:
Ví dụ minh họa:
Cho hàm số y = (m - 2)x + 3. Tìm giá trị của m để hàm số là hàm số bậc nhất và đường thẳng biểu diễn hàm số song song với đường thẳng y = 2x - 1.
Giải:
Để hàm số y = (m - 2)x + 3 là hàm số bậc nhất, ta cần có m - 2 ≠ 0, tức là m ≠ 2.
Để đường thẳng biểu diễn hàm số y = (m - 2)x + 3 song song với đường thẳng y = 2x - 1, ta cần có m - 2 = 2, tức là m = 4.
Vậy, với m = 4, hàm số y = (m - 2)x + 3 là hàm số bậc nhất và đường thẳng biểu diễn hàm số song song với đường thẳng y = 2x - 1.
Để nắm vững kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, các em nên luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Dưới đây là một số bài tập gợi ý:
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, các em nên:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc giải bài tập về hàm số bậc nhất. Chúc các em học tập tốt!